Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





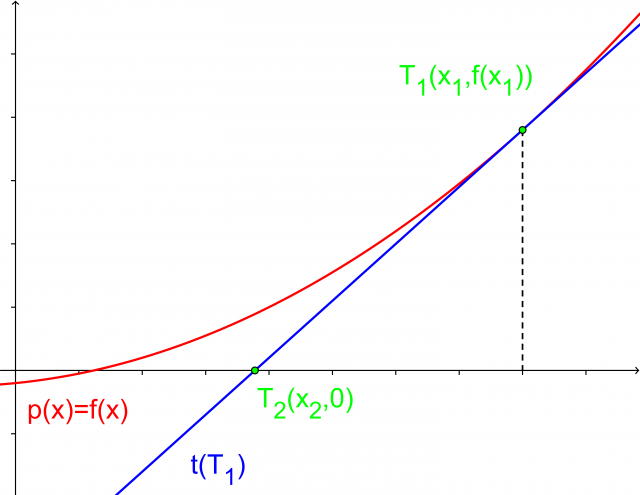
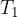 . Calcoliamo la pendenza della tangente (linea blu):
. Calcoliamo la pendenza della tangente (linea blu):