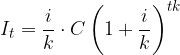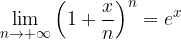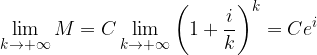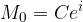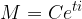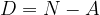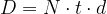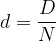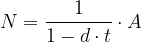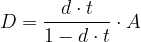Nella vita quotidiana si ha a che fare spesso con prestiti o investimenti che possono maturare periodicamente degli interessi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In questo capitolo svilupperemo con strumenti matematici elementari l'argomento.
Prestazioni finanziarie
Una prestazione finanziaria è un importo monetario datato cioè una coppia ordinata (C , t) dove C è l'importo e t l'istante di tempo in cui esso è "avvenuto".
Se C > 0 allora è un entrata, mentre se C < 0 è un costo (una spesa).
Due prestazioni sono equivalenti quando non abbiamo una preferenza nel sceglierne una o l'altra:
Se invece preferiamo la prima:
Diamo alcuni punti di partenza per dedurre delle condizioni sull'equivalenza e l'ordine:
Un importo nullo non altera mai in nessun modo la situazione finanziaria ovvero non fa differenza se ieri, oggi o domani non ho affrontato nessuna : 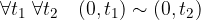
Più denaro posseggo ad un certo istante più sto bene: 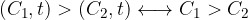
Meglio avere entrate prima e costi poi: 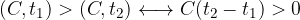
Le regole che stabiliscono l'equivalenza tra prestazioni si chiamano regimi finanziari: date due prestazioni 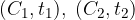 con 3 quantità note su 4, sono le regole per determinarne la rimanente in maniera tale che
con 3 quantità note su 4, sono le regole per determinarne la rimanente in maniera tale che 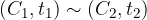 .
.
Capitalizzazione e Attualizzazione
Date due prestazioni equivalenti:
Più precisamente capitalizzazione è determinare la funzione:
Mentre attualizzazione è determinare la funzione:
Risulta più semplice supporre che se due prestazioni sono equivalenti allora rimangano tali moltiplicandole per la stessa costante strettamente positiva.
ovvero i capitali sono proporzionali:
La funzione U dipendente solo dagli istanti 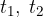 si chiama fattore montante.
si chiama fattore montante.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Risulta ancora più semplice supporre che due prestazioni siano equivalenti allora rimangano tali traslandole nel futuro o nel passato di uno stesso intervallo di tempo.
ovvero il fattore montante dipende solo dalla distanza degli istanti 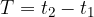 :
:
Riscrivendo l' uguaglianza esplicitando 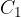 otteniamo:
otteniamo:
La funzione v si chiama fattore di sconto.
Fattore di sconto e fattore montante sono strettamente legati:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Capitale, Montante, Interesse
Si chiama capitale iniziale un importo all'istante t = 0 ovvero le coppie (C, 0), mentre un importo incognito M nel futuro (t > 0) si chiama montante che dipende in generale dall'instante in cui è considerato (M = M(t)).
Un montante M al tempo t di capitale iniziale C è equivalente ad esso:
e come dedotto al capitolo iniziale si ha M > C.
Si chiama interesse la differenza tra montante e capitale iniziale:
Si chiama tasso d'interesse il rapporto tra l'interesse maturato ed il suo capitale iniziale:
spesso tale quantità è espressa come percentuale.
Regimi finanziari
I regimi finanziari più usati sono:
Ad interesse semplice o lineare: il fattore montante è una funzione affine ovvero l'interesse è direttamente proporzionale al tempo trascorso 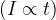
Ad interesse composto: il fattore montante è una funzione esponenziale ovvero l'interesse è funzione esponenziale del tempo trascorso 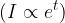
Ad interesse anticipato: il fattore montante è una funzione iperbolica ovvero l'interesse è funzione razionale crescente del tempo trascorso 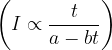
Nei capitoli che seguono dedurremo delle formule esatte, ma negli esempi i risultati saranno approssimati a 2 cifre decimali, quindi alcune verifiche saranno soggette ad errori.
Interesse lineare
In questo regime finanziario l'interesse è direttamente proporzionale al tempo trascorso 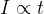
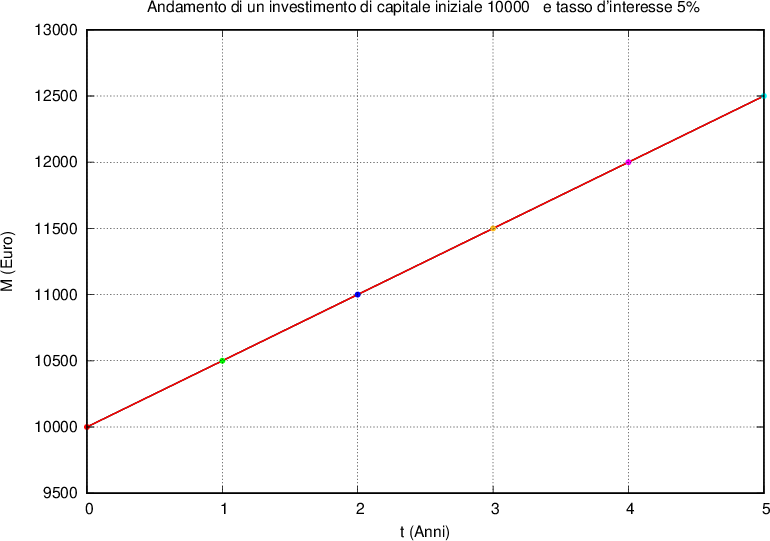
L'interesse I di un capitale iniziale C con regime lineare a tasso d'interesse i all'istante t è dato da:
quindi il montante all'instante t è dato da:
L'andamento è rappresentato in un diagramma cartesiano di variabili tempo - montante da una retta.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Interesse composto
Nel regime lineare non c'è la possibilità di convertire in capitale gli interessi maturati ed aggiungerlo a quello iniziale, mentre nel regime esponenziale avviene ciò.
A seconda che la capitalizzazione sia calcolata annualmente o più frequentemente si dice annua o frazionata.
Capitalizzazione annua
Supponiamo che alla fine di ogni anno l'interesse maturato sia convertito in capitale ed aggiunto a quello iniziale:
Inoltre l'interesse è lineare e calcolato sul capitale accumulato:
Il prospetto dei capitali e degli interessi.
L'interesse I annuale di un capitale iniziale C con regime composto a tasso d'interesse i dopo t anni è dato da:
quindi il montante (o il nuovo capitale) nell'anno t è dato da:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Capitalizzazione frazionata
Spesso le banche non calcolano l'interesse maturato annualmente, ma semestralmente,mensilmente, giornalmente, ecc.
Se la conversione degli interessi è applicata ogni  -esimo di anno e il tasso d'interesse è frazionato per la stessa quantità
-esimo di anno e il tasso d'interesse è frazionato per la stessa quantità 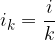 allora dopo un anno il montante è:
allora dopo un anno il montante è:
mentre dopo t anni diventa:
L'interesse I frazionato in k periodi di un capitale iniziale C con regime composto a tasso d'interesse frazionato  dopo t anni è dato da:
dopo t anni è dato da:
quindi il montante (o il nuovo capitale) dopo t anni è dato da:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
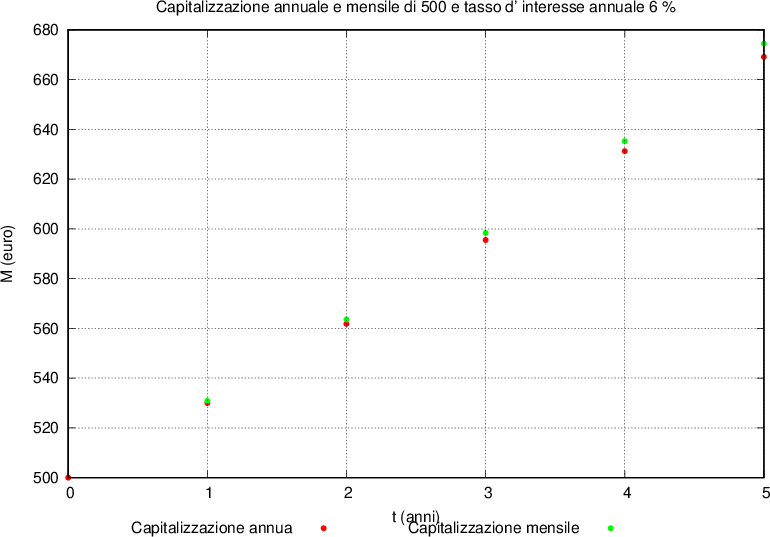
L'andamento in entrambi i casi è rappresentato in un diagramma cartesiano di variabili tempo - montante da una poligonale.
Capitalizzazione continua
Nel capitolo precedente abbiamo visto il montante di un capitale C a regime composto con tasso d'interesse i applicato ogni  -esimo di anno:
-esimo di anno:
Cosa succede se volessimo aumentare arbitrariamente le suddivisioni, cioè sapere in qualunque istante il montante?
Nel capitolo dedicato abbiamo incontrato il numero di Nepero e la funzione esponenziale:
Applichiamo tale limite al nostro caso:
Quindi il montante "istantaneo" ha andamento esponenziale.
Il montante "istantaneo" di un capitale C a capitalizzazione continua con tasso d'interesse i è dato da:
Il montante dopo t anni risulta:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
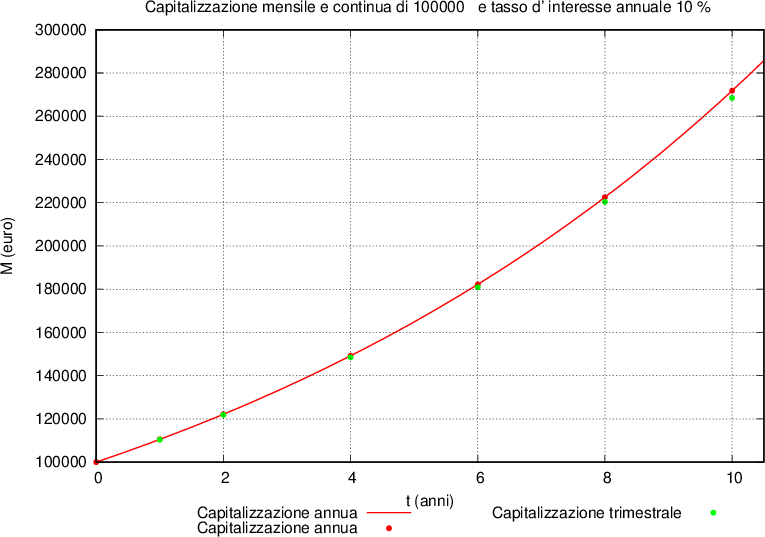
L'andamento è rappresentato in un diagramma cartesiano di variabili tempo - montante da una curva esponenziale per la capitalizzazione continua e una poligonale per quella composta.
Interesse anticipato
Una soluzione possibile per incassare subito una cambiale di valore nominale N all'epoca t è quello di attualizzare tale valore.
Per incassare in anticipo il valore effettivo del titolo finanziario posseduto ci rivolgiamo ad un istituto di credito che ci pagherà il valore attuale in attesa di ritornare in possesso - allo scadere del titolo - della somma N.
La differenza tra il valore attuale A e la somma disponibile N si chiama sconto:
Esso coincide come valore all'interesse, ma si differisce da esso in quanto i ruoli di N e A non sono di montante futuro e capitale iniziale, ma di valore nominale e valore attuale.
La banca che si incarica di anticiparci i soldi, applica uno sconto al valore nominale e nel caso più semplice esso è proporzionale - come l'interesse lineare - alla scadenza:
Similmente al tasso d'interesse i, la costante d si chiama tasso di sconto:
Riscriviamo le formule precedenti in termini di sconto, valore nominale e valore attuale.
Il valore nominale N con regime iperbolico a tasso di sconto d all'istante t di un titolo di valore attuale A è dato da:
quindi il fattore di sconto all'instante t è dato da:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





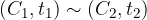
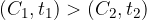
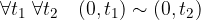
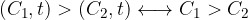
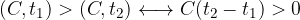
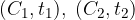 con
con 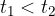 e
e  sono equivalenti, allora
sono equivalenti, allora 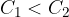
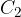 mediante
mediante 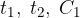 , mentre l'attualizzazione è la determinazione di
, mentre l'attualizzazione è la determinazione di 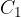 mediante
mediante 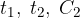 .
.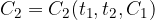
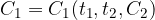
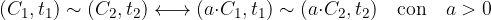
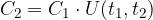
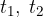 si chiama fattore montante.
si chiama fattore montante.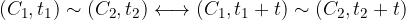
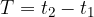 :
: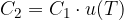
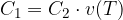
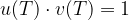
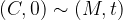
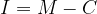
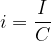
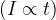
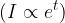
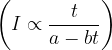
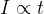
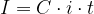
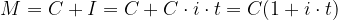
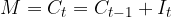
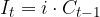
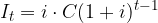
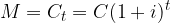
 -esimo di anno e il tasso d'interesse è frazionato per la stessa quantità
-esimo di anno e il tasso d'interesse è frazionato per la stessa quantità 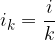 allora dopo un anno il montante è:
allora dopo un anno il montante è: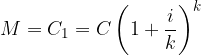
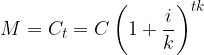
 dopo t anni è dato da:
dopo t anni è dato da: