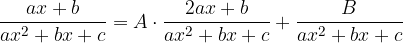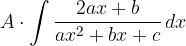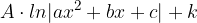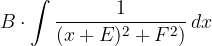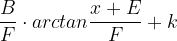Il calcolo dell'integrale indefinito è l'operazione inversa a quella della derivazione.
Consiste nella ricerca della famiglia di funzioni le cui derivate sono uguali alla funzione data.
Come una salita percorsa nel senso inverso è una discesa, così l'integrale indefinito è l'inverso della derivata.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Una funzione F(x) che derivata dà f(x) si chiama primitiva rispetto ad f(x), possiamo descrivere la formula dell'integrale indefinito come:
Visto che la derivata di una costante è uguale a zero, anche tutte le funzioni ottenute dalla primitiva sommando o sottraendo una costante sono soluzioni dell’integrale: si aggiunge quindi una costante arbitraria k alla soluzione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Principali integrali indefiniti
Di seguito è riportata la tabella dei principali integrali indefiniti.
Proprietà degli integrali
Vediamo le proprietà principali degli integrali.
Prodotto per una costante
L’integrale del prodotto di una funzione per una costante è uguale al prodotto della costante per l’integrale della funzione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Somma di integrali
L’integrale di una somma (o sottrazione) di funzioni è uguale alla somma (o sottrazione) degli integrali delle singole funzioni.
Metodi di integrazione
Per risolvere efficacemente gli integrali è necessario capire quale è il metodo più adatto allo scopo.
Integrazione per sostituzione
Il metodo di sostituzione è molto utile per risolvere funzioni composte. Seppure la sua spiegazione possa sembrare leggermente complicata, il suo uso nella pratica si può rivelare decisamente più semplice.
Il primo passo è l'opportuna scelta di una funzione invertibile g tale che la sostituzione x = g(t) possa semplificare la funzione composta iniziale f(x).
Contestualmente alla sostituzione si calcola il differenziale nella nuova variabile d'integrazione t: semplicemente derivando a destra e sinistra l'eguaglianza x = g(t) si ottiene dx = g'(t) dt.
L'integrale iniziale si può ora riscrivere così nella variabile t:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Integrazione per parti
Il metodo di integrazione per parti si usa per risolvere quegli integrali la cui funzione è il prodotto di due funzioni f e g, entrambe derivabili.
Partendo dalla definizione di derivata di funzione composta possiamo dimostrare la formula.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Integrazione di funzioni fratte
Quando la funzione integrale è composta dalla divisione di due polinomi allora possiamo applicare regole apposite.
dove 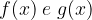 sono polinomi in x.
sono polinomi in x.
Consideriamo i gradi dei due polinomi, si possono presentare 2 casi:
Grado del numeratore maggiore o uguale al grado del denominatore
Se il grado di f è maggiore a quello di g è possibile eseguire la divisione tra polinomi ottenendo il quoziente Q(x) e il resto R(x) tali che:
Quindi l'integrale iniziale si può scrivere come la somma di due integrali.
In questo modo otteniamo un integrale di una funzione non fratta Q(x) e quello di una funzione fratta in cui il numeratore ha grado minore del denominatore e possiamo, se la difficoltà lo richiede, ricondurci al secondo caso.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Grado del numeratore minore del grado del denominatore
In caso di funzioni polinomiali di secondo grado, l'integrale da risolvere è del tipo:
Possiamo distinguere, in base al valore del discriminante tre casi:
Denominatore con due radici reali distinte
Se 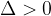 si hanno come soluzioni due radici reali distinte possiamo quindi dire che:
si hanno come soluzioni due radici reali distinte possiamo quindi dire che:
Per trovare A e B utilizziamo il Principio di Identità dei Polinomi
Possiamo adesso utilizzare il seguente sistema:
Una volta risolto sostituiamo nell'integrale di partenza ottenendo:
Denominatore con una radice reale
Se 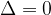 si hanno come soluzioni due radici reali coincidenti possiamo quindi dire che:
si hanno come soluzioni due radici reali coincidenti possiamo quindi dire che:
Procediamo come nel caso precedente.
Denominatore con due radici complesse coniugate
Se 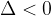 allora il denominatore non può essere scomposto possiamo però portare la nostra frazione nella forma:
allora il denominatore non può essere scomposto possiamo però portare la nostra frazione nella forma:
Ricaviamo quindi A e B utilizzando anche in questo caso il Principio di Identità dei Polinomi
Possiamo in seguito risolvere il primo addendo:
In modo da poter utilizzare la formula di integrazione per gli integrali principali ottenendo:
Invece per il secondo addendo dobbiamo trovare dei valori E e F tali che:
In modo da poter calcolare il seguente integrale ottenendo:





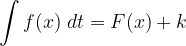
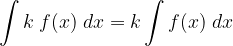
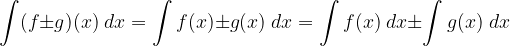
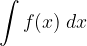
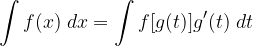
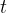 sostituiamo ad esso la funzione inversa di g applicata a x,
sostituiamo ad esso la funzione inversa di g applicata a x, 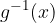 (infatti da
(infatti da 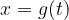 si ha
si ha 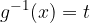 ), ottenendo la soluzione dell'integrale nella variabile di partenza x.
), ottenendo la soluzione dell'integrale nella variabile di partenza x.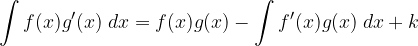
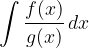
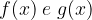 sono polinomi in x.
sono polinomi in x.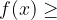 grado
grado 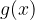
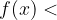 grado
grado 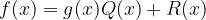
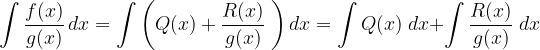
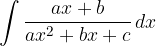
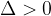 si hanno come soluzioni due radici reali distinte possiamo quindi dire che:
si hanno come soluzioni due radici reali distinte possiamo quindi dire che: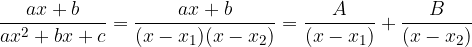
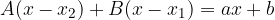
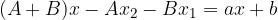
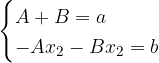
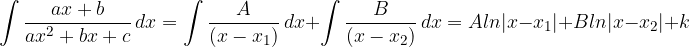
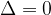 si hanno come soluzioni due radici reali coincidenti possiamo quindi dire che:
si hanno come soluzioni due radici reali coincidenti possiamo quindi dire che: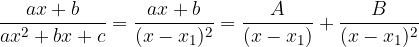
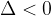 allora il denominatore non può essere scomposto possiamo però portare la nostra frazione nella forma:
allora il denominatore non può essere scomposto possiamo però portare la nostra frazione nella forma: