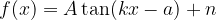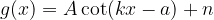Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





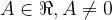 . Ne ricaviamo la nuova funzione:
. Ne ricaviamo la nuova funzione: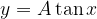
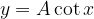
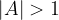 , si ha la dilatazione della funzione lungo l'asse y;
, si ha la dilatazione della funzione lungo l'asse y;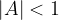 , si ha la contrazione della funzione lungo l'asse y.
, si ha la contrazione della funzione lungo l'asse y.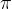 della funzione.
della funzione. , la funzione si dilata lungo l'asse x;
, la funzione si dilata lungo l'asse x; , la funzione si contrae lungo l'asse x.
, la funzione si contrae lungo l'asse x.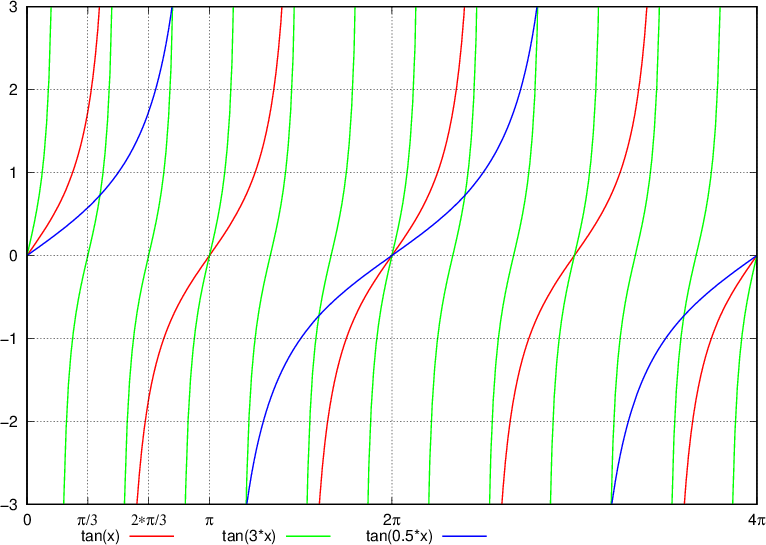
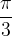 (infatti a
(infatti a 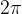 ( infatti a
( infatti a 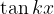 o
o 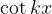 è
è 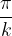 .
. , il periodo è minore di
, il periodo è minore di 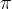
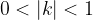 , il periodo è maggiore di
, il periodo è maggiore di