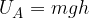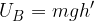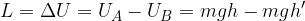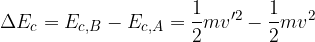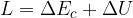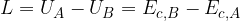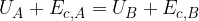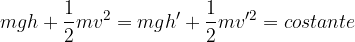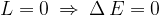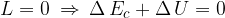L’energia meccanica si presenta sotto due forme: energia potenziale ed energia cinetica.
La prima è un’energia “di posizione”, la seconda “di movimento”.
L'energia potenziale di un corpo
Osserviamo la figura e calcoliamo il lavoro compiuto dal corpo per arrivare a terra (prima seguendo il piano inclinato e poi seguendo la traiettoria verticale):
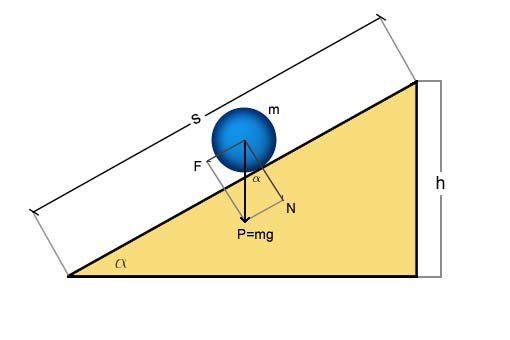
Un corpo di massa m su un piano inclinato
Consideriamo prima il lavoro L compiuto dalla componente F lungo la direzione dello spostamento s della forza peso P:
F è la componente parallela alla direzione s di P, quindi possiamo scrivere F in funzione di P:
Calcoliamo ora lo stesso lavoro L considerando lo spostamento h:
Dato che il lavoro deve essere lo stesso abbiamo:
Il lavoro, in un campo conservativo (come quello gravitazionale), è indipendente dalla traiettoria percorsa, dipende soltanto dal punto di inizio e di fine del percorso. Questo significa che se il punto di inizio e fine coincidono il lavoro è nullo.
Cosa esprime L? Esprime la misura dell’energia potenziale che possiede un corpo che si sposta da una quota h a una quota di riferimento.
Nel campo della gravità possiamo assumere come riferimento il livello del mare, quindi:
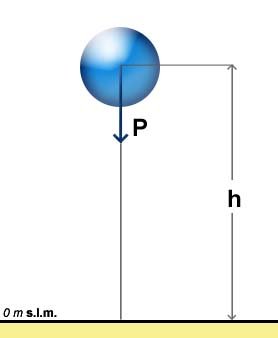
un corpo di peso P che si trovi a un’altezza h sul livello del mare, ha un’energia potenziale U pari a:
O, in termini di massa,dato che P=mg:
L’energia potenziale è l’energia posseduta da un corpo in relazione alla sua posizione rispetto a una posizione di riferimento.
Viene indicata con U e la sua unità di misura è il Joule [J]
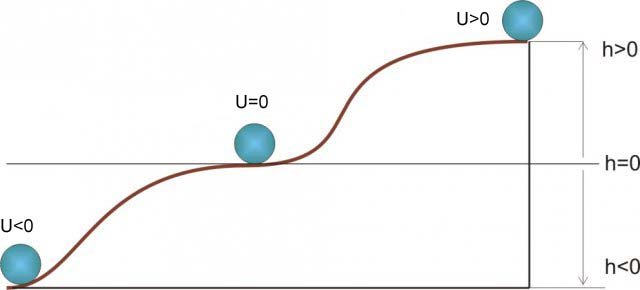
Figura 1: L'energia potenziale può essere positiva, negativa o pari a zero rispetto alla posizione di riferimento.
L'energia potenziale del corpo varia in funzione della sua altezza rispetto a un piano di riferimento:
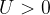 se l'altezza h è maggiore alla quota di riferimento
se l'altezza h è maggiore alla quota di riferimento
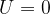 , quando il corpo si trova alla quota di riferimento
, quando il corpo si trova alla quota di riferimento
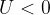 , se l'altezza h è inferiore alla quota di riferimento
, se l'altezza h è inferiore alla quota di riferimento
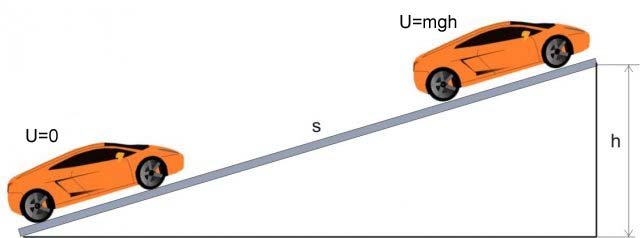
Figura 2: Un'automobile percorre una strada in pendenza
All'inizio della strada la macchina ha un'energia potenziale pari a zero, in cima alla salita la sua energia potenziale è U=mgh.
La legge di conservazione dell'energia
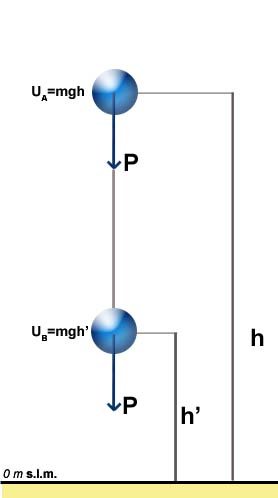
Un corpo di massa m cade da un punto A a un'altezza h fino a un punto B a un'altezza h'.
L'energia potenziale in A è quindi:
dopo la caduta in B invece:
Il lavoro che ha compiuto quindi è pari alla differenza di energia potenziale:
Se nel punto A aveva una velocità v e in B una velocità v' possiamo anche calcolare la variazione di energia cinetica:
Per il teorema dell'energia cinetica questa variazione è proprio pari al lavoro L compiuto per andare da A a B.
Possiamo allora eguagliare le due espressioni di L:
Questa equazione esprime il Teorema della conservazione dell'energia:
Teorema della conservazione dell'energia
In un campo di forza conservativo la somma dell'energia potenziale e cinetica è costante.
Chiariamo il Teorema con un esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La legge si applica in generale a tutti i tipi di energia. Per ora, verrà utilizzato solo per l'energia cinetica e potenziale:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'esempio precedente ci permette di riflettere su un'importante questione: molto spesso possiamo giungere alla soluzione di un problema di fisica passando da strade diverse; infatti, in questo caso, il problema poteva essere anche risolto utilizzando l'equazione che descrive la caduta libera dei gravi.





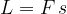
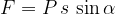
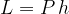
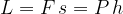
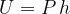
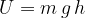

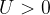 se l'altezza h è maggiore alla quota di riferimento
se l'altezza h è maggiore alla quota di riferimento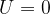 , quando il corpo si trova alla quota di riferimento
, quando il corpo si trova alla quota di riferimento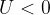 , se l'altezza h è inferiore alla quota di riferimento
, se l'altezza h è inferiore alla quota di riferimento