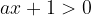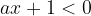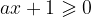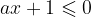La disequazione è una diseguaglianza che è verificata per certi intervalli di valori
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Maggiore e minore
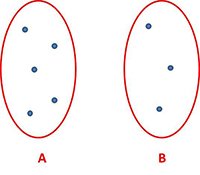
Alla base del concetto di disequazione c'è quello di maggiore (>) e minore (<). I due simboli derivano dalla teoria degli insiemi. Supponiamo di avere due insiemi (A e B).
Andiamo a contare gli elementi all'interno di ciascun insieme, creando con questi elementi due colonne (A e B).
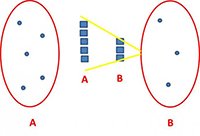
Ora congiungiamo gli estremi delle colonne. In questo modo si ottiene il simbolo maggiore (>):
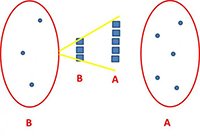
Così invece si ottiene il simbolo minore (<):
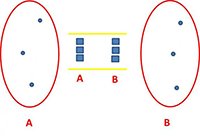
Se gli insiemi contengono lo stesso numero di oggetti, con lo stesso procedimento usato in precedenza otteniamo il simbolo uguale (=):
Tipi di disequazioni
Per quanto riguarda i termini utilizzati: primo membro, secondo membro, incognita, grado essi hanno lo stesso significato che presentano nel caso delle equazioni.
Altrettanto si può dire delle proprietà (sommando/sottraendo la stessa quantità ai due membri, moltiplicando/dividendo per un numero diverso da zero entrambi i membri il risultato non cambia).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Come per le equazioni, anche nel caso delle disequazioni esistono quelle di grado superiore al primo.
Risolvere una disequazione di primo grado
Mentre nel caso di un’equazione di primo grado la soluzione (se esiste) è unica, nel caso di una disequazione la soluzione è, alternativamente:
un insieme di valori reali (un intervallo, a volte infinito, di valori);
l’insieme vuoto, quindi nessun valore.
La ricerca delle soluzioni,di una disequazione di primo grado si effettua con le stesse modalità con cui si affronta un’equazione di primo grado: si trasportano tutti i termini contenenti la 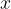 a primo membro e quelli privi della
a primo membro e quelli privi della 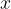 a secondo membro.
a secondo membro.
Bisogna tenere presente una regola fondamentale nelle disequazioni: nel caso in cui a primo membro il coefficiente della 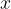 sia negativo occorre:
sia negativo occorre:
moltiplicare per 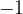 sia il primo che il secondo membro;
sia il primo che il secondo membro;
cambiare il verso della disuguaglianza, così che  diventi
diventi  (e viceversa).
(e viceversa).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Perchè giriamo il segno di maggiore e minore quando moltiplichiamo entrambi i membri per un numero negativo? E' facile se consideriamo questo esempio. E' vero che 8 e maggiore di 4.
Moltiplichiamo entrambi i numeri per - 1 e ci accorgiamo che l'espressione matematica è falsa.
Infatti -8 è minore di -4. L'espressione diventa dunque, scambiando il maggiore con un minore:
Le disequazioni di primo grado intere
Le disequazioni di primo grado intere sono quelle in cui l'incognita si trova solo al numeratore. Il procedimento utilizzato per risolvere tali disequazioni è il seguente:
Procedimento per risolvere una disequazione di primo grado intera:
Si spostano i termini con la 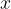 al primo membro e quelli senza la
al primo membro e quelli senza la 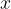 al secondo membro. I termini che si spostano da un membro all'altro devono essere cambiati di segno, quelli che non si spostano restano con lo stesso segno.
al secondo membro. I termini che si spostano da un membro all'altro devono essere cambiati di segno, quelli che non si spostano restano con lo stesso segno.
Si sommano i termini simili.
Se davanti alla 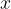 c’è un numero negativo si cambiano i segni e si gira il verso della disequazione.
c’è un numero negativo si cambiano i segni e si gira il verso della disequazione.
Si dividono ambo i membri per il numero davanti alla 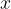 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Un caso particolare di fronte al quale ci si può trovare è quello in cui la 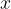 scompare. In questo caso a primo membro c’è lo zero ed a secondo membro un numero.
scompare. In questo caso a primo membro c’è lo zero ed a secondo membro un numero.
Si hanno quindi due possibilità:
La disequazione che ne risulta è vera: allora tutti i valori della 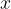 sono soluzioni. La disequazione si dice INDETERMINATA. Ad esempio:
sono soluzioni. La disequazione si dice INDETERMINATA. Ad esempio:
La disequazione che ne risulta è falsa: allora nessun valore della 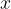 è soluzione. La disequazione si dice IMPOSSIBILE. Ad esempio:
è soluzione. La disequazione si dice IMPOSSIBILE. Ad esempio:
Le disequazioni di primo grado fratte
Le disequazioni di primo grado fratte sono quelle in cui l'incognita compare al denominatore. Esse si presentano nella forma:
Bisogna ricordare in questo caso, come accade per le equazioni, che:
E' assolutamente vietato dividere un numero per 0. Bisogna quindi escludere dalle possibili soluzioni tutti i valori che annullano il denominatore.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il procedimento utilizzato per risolvere questo tipo di equazioni è il seguente:
Si studiano separatamente numeratore e denominatore studiando quando entrambi sono 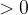 indipendentemente dal verso della disequazione.
indipendentemente dal verso della disequazione.
Si spostano i termini con la 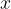 a 1° membro e quelli senza la
a 1° membro e quelli senza la 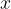 a secondo membro. I termini che si spostano da un membro all'altro devono essere cambiati di segno, quelli che non si spostano restano con lo stesso segno.
a secondo membro. I termini che si spostano da un membro all'altro devono essere cambiati di segno, quelli che non si spostano restano con lo stesso segno.
Si sommano i termini simili.
Se davanti alla 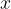 c’è un numero negativo si cambiano i segni e si gira il verso della disequazione.
c’è un numero negativo si cambiano i segni e si gira il verso della disequazione.
Si dividono ambo i membri per il numero davanti alla 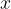 .
.
I risultati così trovati si pongono in una tabella contenente linee continue oppure tratteggiate analogamente a quanto visto per le disequazioni intere: una riga riguarderà il numeratore,l'altra il denominatore.
L'insieme delle soluzioni sarà dato dagli intervalli in cui l'intera frazione assume il segno richiesto dall'esercizio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Disequazioni indeterminate
Ci possono essere due casi di disequazione indeterminata:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Disequazioni impossibili
Ci possono essere due casi di disequazione impossibile:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Disequazioni letterali
Le disequazioni letterali sono quelle in cui compaiono altre lettere oltre all'incognita, del tipo:
Il procedimento è lo stesso utilizzato per risolvere le disequazioni intere e fratte.
Ci sono però due differenze:
Nel risultato spesso ci sono delle lettere al denominatore. In questi casi bisogna discutere la soluzione.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »






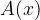 e
e 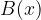 , entrambi di primo grado in
, entrambi di primo grado in 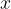 , come segue:
, come segue: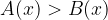
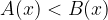
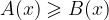
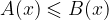
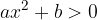
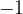 sia il primo che il secondo membro;
sia il primo che il secondo membro; diventi
diventi  (e viceversa).
(e viceversa).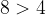

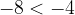
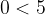
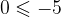
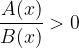
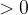 indipendentemente dal verso della disequazione.
indipendentemente dal verso della disequazione.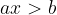 , con
, con 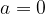 e
e 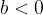 . Infatti in questo caso avremo
. Infatti in questo caso avremo 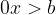 ovvero
ovvero 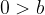 e lo zero è sempre maggiore di un qualsiasi numero negativo.
e lo zero è sempre maggiore di un qualsiasi numero negativo.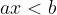 , con
, con 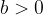 . Infatti in questo caso avremo
. Infatti in questo caso avremo 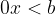 ovvero
ovvero 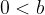 e lo zero è sempre minore di un qualsiasi numero positivo.
e lo zero è sempre minore di un qualsiasi numero positivo.