Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




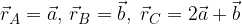
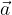 e
e 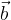 calcolare i vettori:
calcolare i vettori: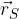
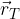
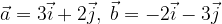
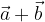
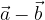
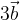
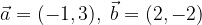
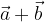
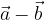
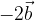
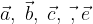
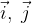
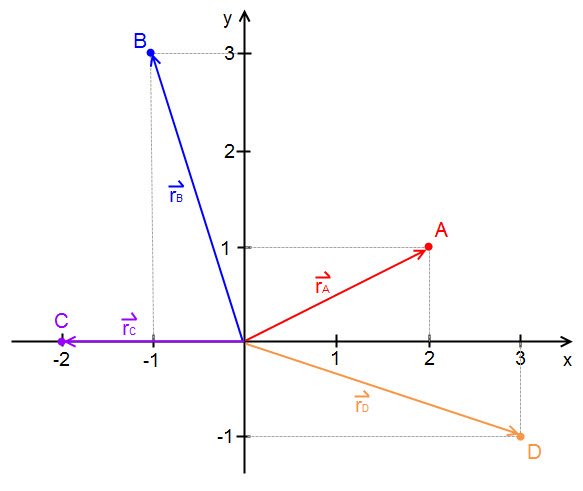
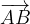
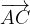
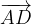
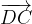
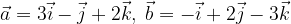
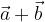
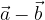
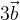
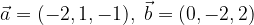
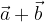
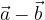
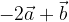
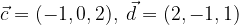
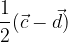
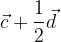
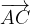
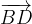
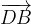
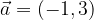 e
e 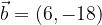
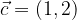 e
e 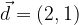
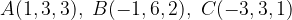
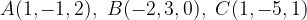
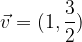 . Per quale valore dello scalare m il vettore mv è un vettore locale appartenente a p?
. Per quale valore dello scalare m il vettore mv è un vettore locale appartenente a p?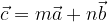 ha come componenti
ha come componenti 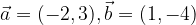 e
e 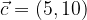 .
.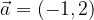 e
e 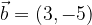 trovare il vettore
trovare il vettore 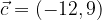 .
.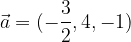 e
e 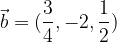 sono paralleli.
sono paralleli.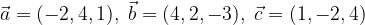
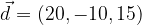
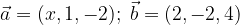
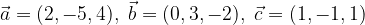
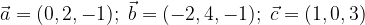
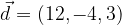
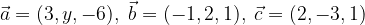
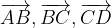 e
e 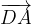 sono complanari?
sono complanari?


