Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti




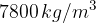 .
.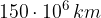 . Qual è la risultante delle forze gravitazionali agenti sulla Luna? La massa della Terra è
. Qual è la risultante delle forze gravitazionali agenti sulla Luna? La massa della Terra è 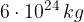 , la massa del sole è 330.000 volte più grande e la massa della Luna era di 81 volte più piccolo della massa della Terra.
, la massa del sole è 330.000 volte più grande e la massa della Luna era di 81 volte più piccolo della massa della Terra.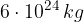 , la massa della Luna è
, la massa della Luna è 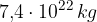 .
.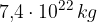 . Quanto pesa un'astronauta sulla luna con una massa di 100 kg?
. Quanto pesa un'astronauta sulla luna con una massa di 100 kg?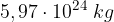
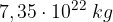
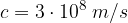
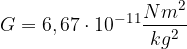
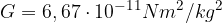 e
e 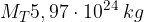 .
.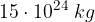 sapendo che dista dal centro del pianeta 950 km . Assumere la costante di gravitazione universale
sapendo che dista dal centro del pianeta 950 km . Assumere la costante di gravitazione universale 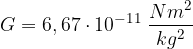 .
.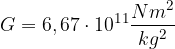
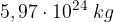 , il raggio della Terra pari a 6371 km e la costante di gravitazione universale G pari a:
, il raggio della Terra pari a 6371 km e la costante di gravitazione universale G pari a: