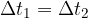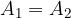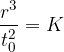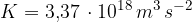Come abbiamo visto nel capitolo precedente i tre principi di Newton ci dicono che le forze svolgono un ruolo fondamentale per lo studio del moto di un corpo. Tutte le forze sono la manifestazione di una o più contemporaneamente forze fondamentali. Esse sono:
Forza Gravitazionale: è quella forza attrattiva che tutti i corpi con la propria massa esercitano nello spazio anche a grandi distanze;
Forza elettrodebole (forza elettromagnetica e forza nucleare debole): la forza elettromagnetica è responsabile dell'interazione tra oggetti che possiedono carica elettrica, invece la forza nucleare debole è responsabile della radioattività della materia. Negli ultimi anni queste due forze seppur tanto diverse, sono state unificate, cioè è stato dimostrato che sono una manifestazione della stessa forza detta appunto elettrodebole.
Forza nucleare forte: è la forza che tiene insieme le particelle che costituiscono il nucleo degli atomi.
In questo capitolo studieremo la forza gravitazionale.
Legge di gravità di Newton
La forza di attrazione tra due masse può essere calcolata utilizzando la legge di gravità di Newton. Questa dice che la forza tra due masse è proporzionale al prodotto delle due masse e inversamente proporzionale al quadrato della loro distanza:
Ci sono due 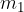 e
e 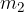 due masse, la distanza r è la distanza tra loro. G è la costante gravitazionale ed è pari a:
due masse, la distanza r è la distanza tra loro. G è la costante gravitazionale ed è pari a:
Questa legge vale solo per le masse puntiformi. Nel caso di corpi estesi invece usiamo il centro di massa.
La forza di attrazione tra due masse puntiformi è calcolata utilizzando la legge di gravitazione universale di Newton:
dove r è la distanza fra le due masse e G è la costante gravitazionale che vale:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Gravità
Una massa m, sulla superficie della Terra, sappiamo che viene attratta con una certa forza detta forza peso:
dove g è l'accelerazione di gravità che vale:
Guardiamo ancora una volta la legge di Newton di gravità:
L'accelerazione di gravità sulla superficie della Terra è:
dove G è la costante gravitazionale, M è la massa della Terra, e R il raggio della Terra.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Come varia la forza di gravità?
Quando ci allontaniamo dalla superficie della terra l'accelerazione gravitazionale diminuisce . Vediamo il seguente schizzo:
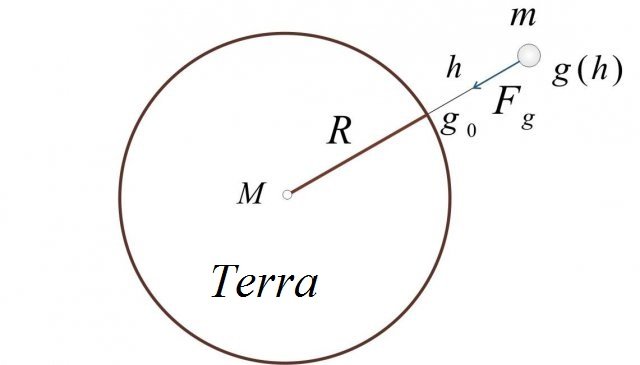
Figura 2: la forza di gravità rispetto alla superficie della Terra.
Alziamoci all'altezza h sopra la superficie della Terra. La nostra distanza dal centro della Terra è:
Applichiamo la legge di gravità di Newton:
Abbiamo ottenuto una formula che ci dice come varia l'accelerazione gravitazionale con l'altitudine:
La forza gravitazionale varia con l'altezza secondo la seguente equazione:
L'accelerazione di gravità in funzione dell'altezza è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Traiettoria dei satelliti
Abbiamo visto nei capitoli precedenti che nei moti circolari la forza centrifuga determina una variazione di direzione.
Un satellite con una massa m ad un'altezza h dalla superficie della Terra rimane in orbita solo se la forza gravitazionale è uguale alla forza centripeta:
L'accelerazione gravitazionale è uguale all'accelerazione radiale. Pensateci: se vogliamo satelliti in orbita intorno alla Terra, le due accelerazioni devono essere necessariamente uguali, altrimenti:
se l'accelerazione gravitazionale è inferiore alla centripeta, il corpo fuggirebbe nello spazio;
se l'accelerazione gravitazionale è maggiore della centripeta, il corpo cadrebbe a terra.
L'accelerazione centripeta viene calcolata utilizzando una delle equazioni disponibili, a seconda dei dati disponibili:
Si è tenuto conto del fatto che la distanza dal centro di rotazione è R + h.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Leggi di Keplero
Prima di Newton, l'astronomo tedesco Johannes Kepler scrisse le tre leggi del moto dei pianeti intorno al sole. Le leggi sono tre e sono chiamate appunto leggi di Keplero.
Prima Legge di Keplero
Legge delle orbite ellittiche : i pianeti si muovono intorno al sole con una traiettoria ellittica e il Sole occupa uno dei fuochi dell'ellisse.
In molti casi, l'ellisse è poco schiacciata tanto da poter essere approssimata a una circonferenza.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Seconda legge di Keplero
Legge delle aree: la congiungente tra il pianeta e il Sole spazza aree uguali in tempi uguali(vedi Figura 3).
Per facilitare la comprensione della legge si disegna il disegno:
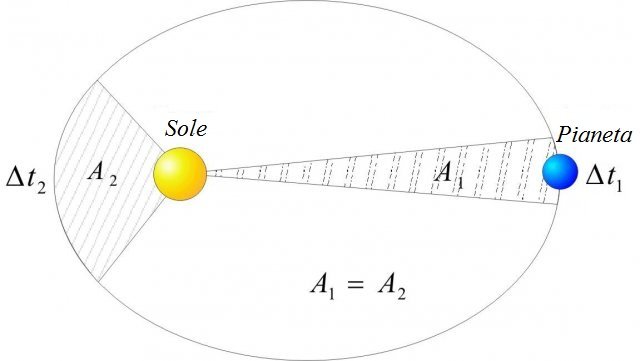
Figura 3: la seconda legge di Keplero.
Nella figura 3, ci siamo concentrati su due punti:
La seconda legge di Keplero dice che se l'intervallo di tempo è uguale, vale a dire:
Ne consegue che descrive le dimensioni dello stesso:
La legge descrive il fatto che i pianeti quando sono più vicini al Sole, si muovono più velocemente, mentre se sono più lontani la velocità è minore.
Terza legge di Keplero
Legge dei periodi:Il quadrato del periodo di rivoluzione di un pianeta attorno al sole è proporzionale al cubo della sua distanza media dal sole.
Egli ha osservato che il rapporto tra la distanza al cubo del pianeta dal Sole e il periodo di rivoluzione per tutti i pianeti è la stessa:
Questo rapporto è detto costante di Keplero ed è pari a:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




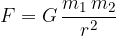
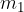 e
e 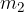 due masse, la distanza r è la distanza tra loro. G è la costante gravitazionale ed è pari a:
due masse, la distanza r è la distanza tra loro. G è la costante gravitazionale ed è pari a: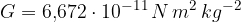
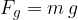
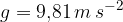
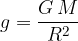

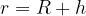

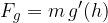
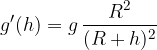
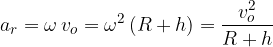

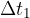 descrive una superficie
descrive una superficie 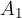 .
.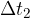 spazza una superficie
spazza una superficie 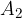 .
.