Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





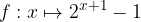
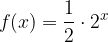
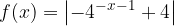
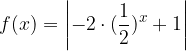
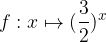
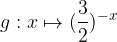
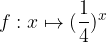
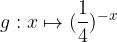
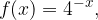
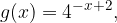
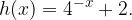
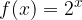
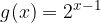
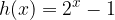
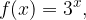
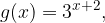
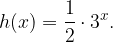
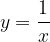
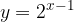
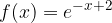
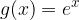
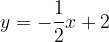
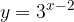
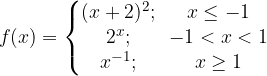
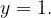
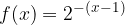
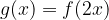
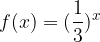
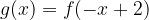
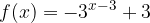 , quindi disegnarne il grafico. Nello stesso sistema di assi cartesiani disegnare anche il grafico della funzione
, quindi disegnarne il grafico. Nello stesso sistema di assi cartesiani disegnare anche il grafico della funzione 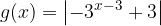
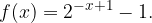
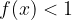
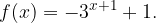
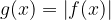
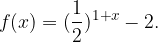
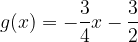 . Determinare l'intervallo per cui
. Determinare l'intervallo per cui 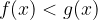
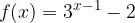
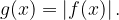
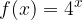 con il vettore di traslazione
con il vettore di traslazione 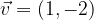 .
.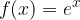 e
e 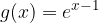 .
.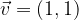 . Determinare l'equazione di h(x).
. Determinare l'equazione di h(x).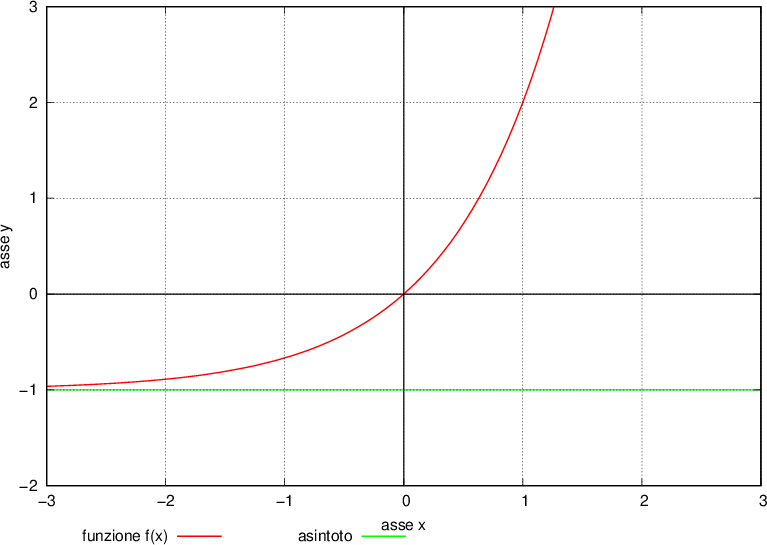
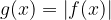 e
e 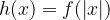
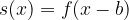 tale che abbia uno zero nel punto di ascissa 2. Trovare il valore di b e l'equazione della funzione s(x).
tale che abbia uno zero nel punto di ascissa 2. Trovare il valore di b e l'equazione della funzione s(x).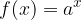 tale che sia
tale che sia 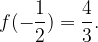
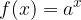 tale che sia
tale che sia 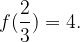
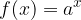 tale che sia
tale che sia 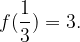
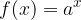 passante per il punto
passante per il punto 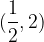 . Una volta trovata l'equazione della funzione f, determinare la sua intersezione con l'asse delle ordinate, l'equazione dell'asintoto orizzontale e disegnarne il grafico.
. Una volta trovata l'equazione della funzione f, determinare la sua intersezione con l'asse delle ordinate, l'equazione dell'asintoto orizzontale e disegnarne il grafico.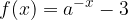
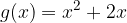
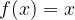 e disegnarne il grafico su carta logaritmica.
e disegnarne il grafico su carta logaritmica.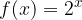 e disegnarne il grafico su carta logaritmica.
e disegnarne il grafico su carta logaritmica.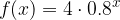 e disegnarne il grafico su carta logaritmica.
e disegnarne il grafico su carta logaritmica.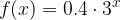 e disegnarne il grafico su carta logaritmica.
e disegnarne il grafico su carta logaritmica.


