Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





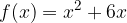
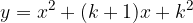 :
: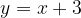
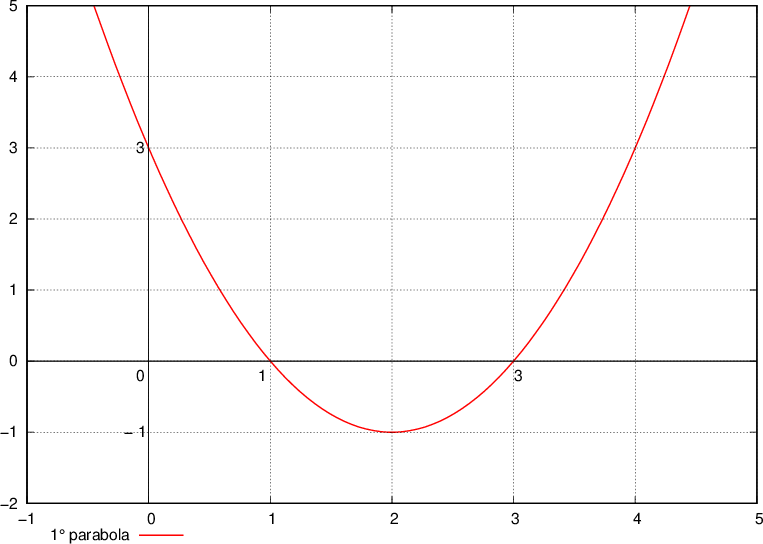
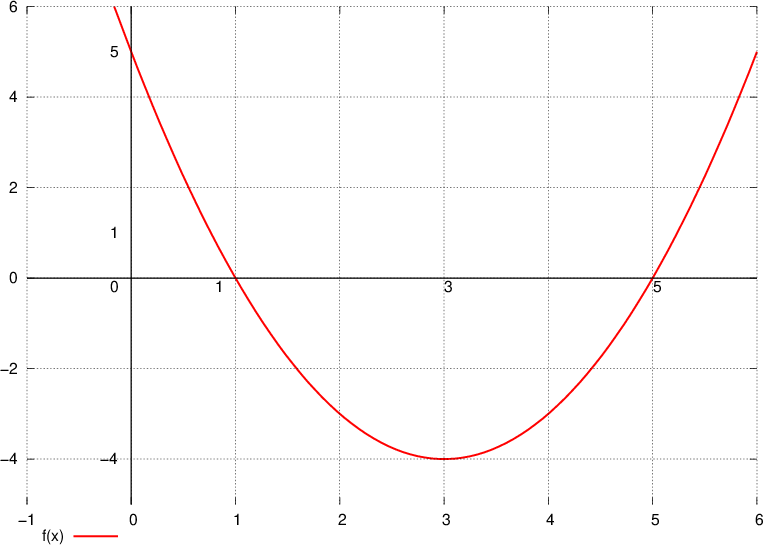
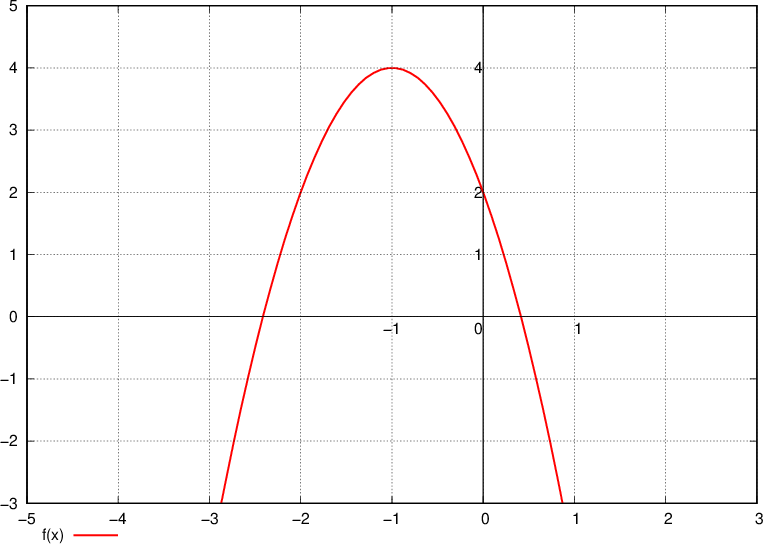
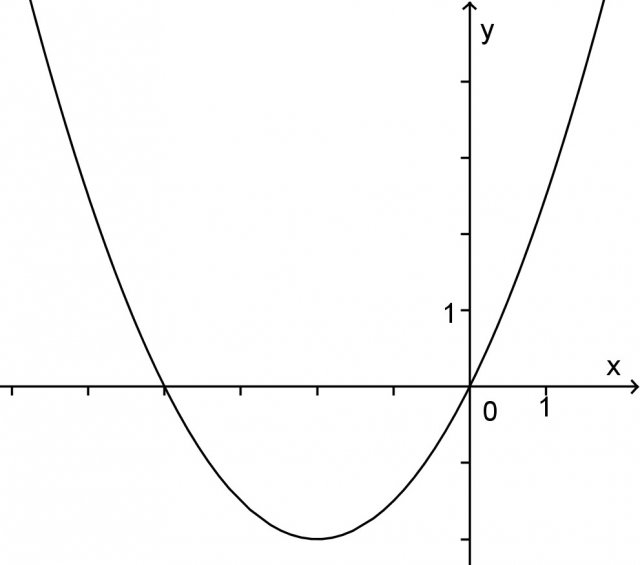
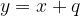 è tangente alla parabola data e quali sono le coordinate del punto di tangenza. Infine, disegnare la parabola e la retta tangente trovata.
è tangente alla parabola data e quali sono le coordinate del punto di tangenza. Infine, disegnare la parabola e la retta tangente trovata.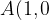 ) e
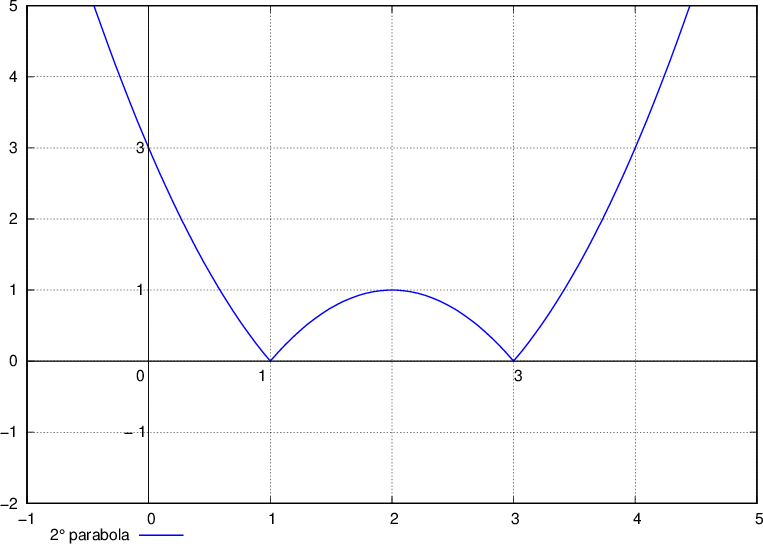
) e 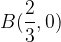 e che sia tangente alla retta
e che sia tangente alla retta 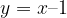 . Infine disegnare la parabola e la retta.
. Infine disegnare la parabola e la retta.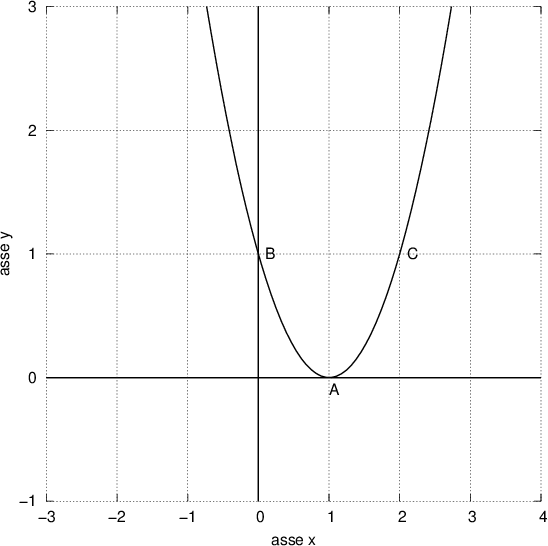
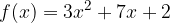
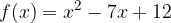
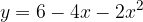
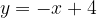
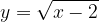
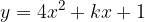
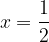
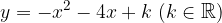
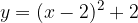
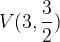
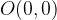
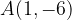
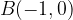
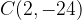

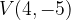
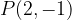
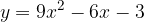
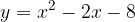
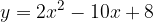
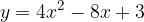
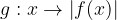
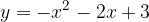
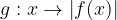
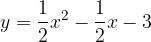
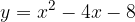
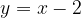
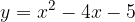
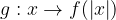
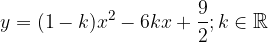
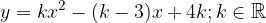
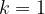
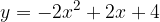
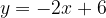
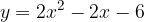
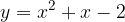
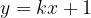
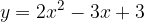
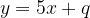
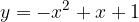
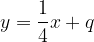
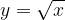
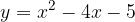
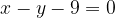
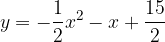
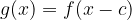
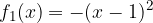
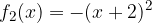
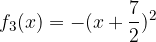
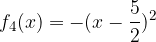
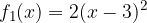
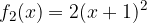
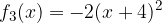
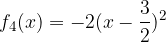
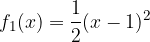
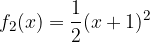
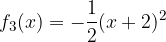
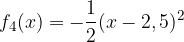
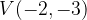
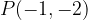
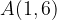
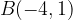
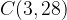
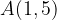
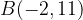
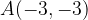
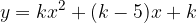
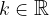
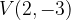
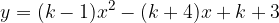
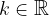
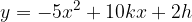
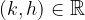
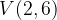
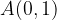
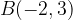
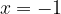
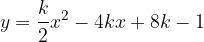
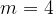
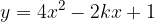
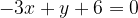
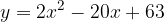
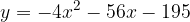
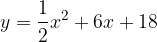
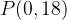
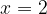
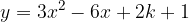
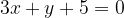
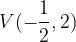
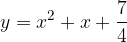
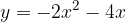
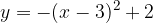
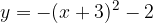
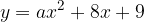
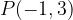
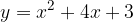
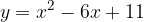
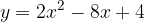
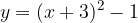
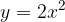
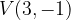
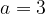
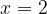
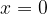
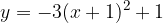
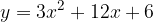
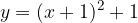
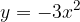
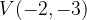
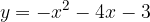
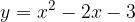
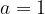
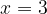
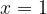
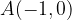
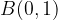
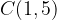
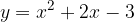
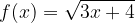
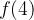
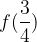
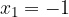
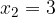
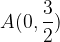
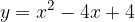
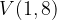
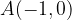
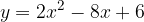
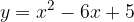

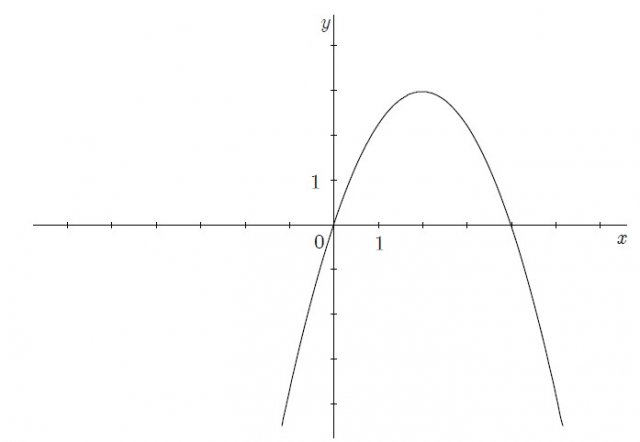
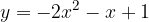
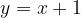
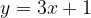
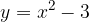
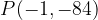
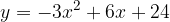
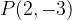
 e - 3, passante per il punto
e - 3, passante per il punto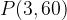
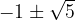 , passante per il punto
, passante per il punto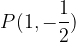

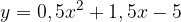
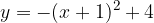
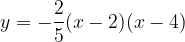
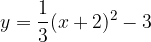
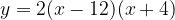
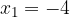
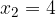
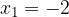
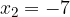
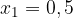
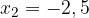
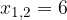
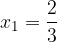
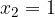
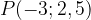
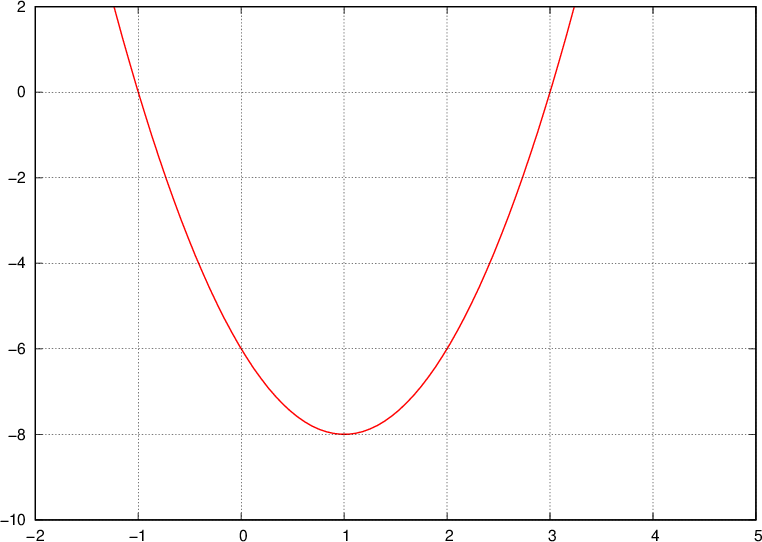
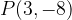
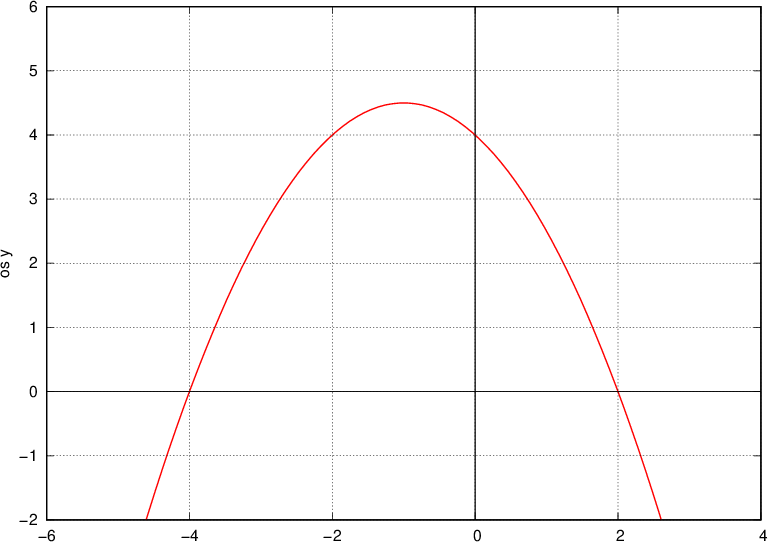
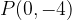 .
.


