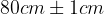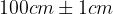Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





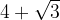
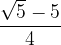

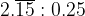
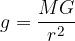
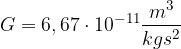 è la costante gravitazionale arrotondata a tre cifre significative, calcolare l'accelerazione di gravità su Marte sapendo che:
è la costante gravitazionale arrotondata a tre cifre significative, calcolare l'accelerazione di gravità su Marte sapendo che: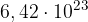 kg
kg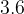 cm
cm cm
cm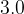 cm
cm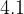 cm
cm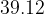
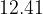
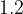
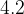
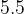
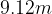
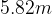
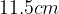
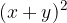
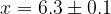 e
e 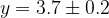

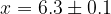 e
e