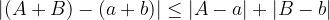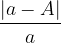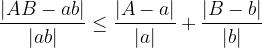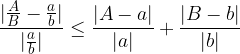Nelle diverse discipline scientifiche (ingegneria, architettura, chimica, ecc.), gli strumenti che vengono utilizzati per effettuare delle misurazioni non consentono mai di ottenere dei valori accurati. Esiste sempre un margine di errore che ci costringe a effettuare delle approssimazioni. Un'approssimazione è comunque una rappresentazione di una determinata grandezza che, pur non essendo completamente esatta, è tuttavia abbastanza precisa da avere un'utilità pratica.
Notazione matematica
Quando si misura una determinata grandezza, possiamo distinguere due valori che si indicano in due modi diversi:
valore approssimato della grandezza misurata, indicato con A
valore esatto della grandezza misurata, indicato con a
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Errori
Distinguiamo due tipi di errori:
Errore assoluto
L'errore assoluto è il limite assoluto entro il quale probabilmente risiede il vero valore della grandezza misurata. Quindi:
L'errore assoluto rappresenta la dimensione dell'errore fatto ed è definito dalla differenza tra il valore misurato e il valore esatto, cioè:
Se indichiamo con  il valore massimo possibile per l'errore assoluto, il valore esatto sarà limitato nel modo seguente:
il valore massimo possibile per l'errore assoluto, il valore esatto sarà limitato nel modo seguente:
In altre parole il valore massimo di a è 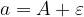 e il valore minimo è
e il valore minimo è 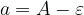 .
.
Nota:  è la lettera greca epsilon.
è la lettera greca epsilon.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Errore assoluto nella somma e nella differenza
Nel calcolo delle approssimazioni, per gli errori assoluti vale la seguente regola:
Se a e b sono i valori esatti di due grandezze e A e B i relativi valori approssimati, allora l'errore assoluto nel calcolare la loro somma (o differenza) è minore o uguale alla somma degli errori assoluti:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Errore relativo
Spesso ci interessa valutare la dimensione dell'errore rispetto al valore esatto di una grandezza. Il rapporto risultante è detto errore relativo.
L'errore relativo ci consente quindi di valutare l'entità di un errore, ovvero se un errore è piccolo o grande e di conseguenza se è più o meno tollerabile. Minore è il valore dell'errore relativo, maggiore sarà la precisione della misurazione effettuata.
L'errore relativo si calcola come rapporto tra l'errore assoluto e valore esatto della grandezza misurata:
L'errore relativo è spesso espresso in percentuale ed è indicato con la lettera r.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Errore relativo di un prodotto e di un quoziente
Per gli errori relativi valgono le seguenti regole:
Se a e b sono i valori esatti di due grandezze e A e B i relativi valori approssimati, allora:
L'errore relativo nel calcolo di un prodotto è minore o uguale alla somma degli errori relativi dei singoli fattori:
L'errore relativo nel calcolo di un quoziente è minore o uguale alla somma degli errori relativi del numeratore e denominatore:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Arrotondamento
Quando non abbiamo bisogno di risultati particolarmente accurati possiamo ricorrere all'arrotondamento. L'arrotondamento consiste nel ridurre il numero delle cifre significative con cui si rappresenta una determinata grandezza.
Per l'arrotondamento valgono le seguenti regole:
se la cifra in corrispondenza della quale si vuole troncare un numero è seguita da 0,1,2,3 o 4, la cifra resta invariata
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
se la cifra in corrispondenza della quale si vuole troncare un numero è seguita da 5,6,7,8 o 9, la cifra viene incrementata di 1
Nota: Se l'ultima cifra da mantenere è 9 e bisogna incrementarla di 1, viene posta a zero e si aumenta di 1 la cifra precedente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Tipi di arrotondamento
Abbiamo due tipi di arrotondamento:
Arrotondamento a n cifre significative:
Arrotondare a n cifre significative significa mantenere le prime n cifre del numero, partendo dalla prima cifra da sinistra che sia diversa da zero.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Arrotondamento a n cifre decimali:
Arrotondare a n cifre decimali significa mantenere le prime n cifre dopo la virgola e impostare le restanti cifre a zero.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nota: quando si svolge una somma, una differenza, un prodotto o un quoziente, di solito si arrotonda il risultato al numero di cifre decimali del fattore con minor numero di cifre decimali.





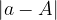
 il valore massimo possibile per l'errore assoluto, il valore esatto sarà limitato nel modo seguente:
il valore massimo possibile per l'errore assoluto, il valore esatto sarà limitato nel modo seguente: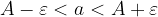
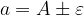
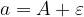 e il valore minimo è
e il valore minimo è 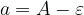 .
.