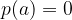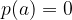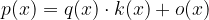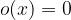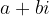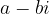Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





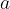 è uno zero per un polinomio, quando il valore del polinomio in questo punto è 0.
è uno zero per un polinomio, quando il valore del polinomio in questo punto è 0.