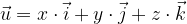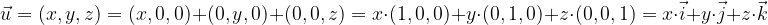Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





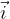 e
e 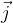 come mostrato in Figura1.
come mostrato in Figura1.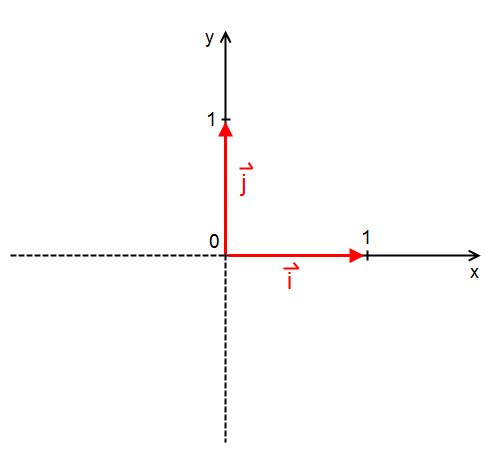
 e
e  come mostrato in Figura2.
come mostrato in Figura2.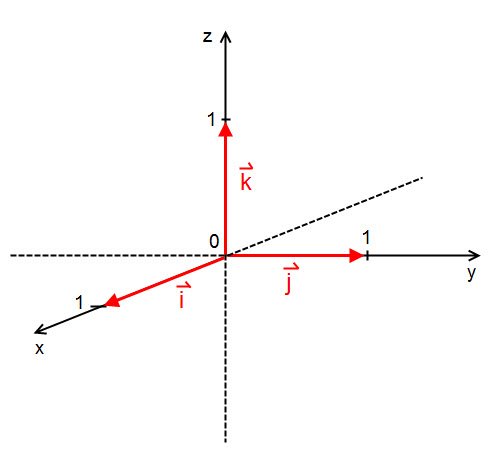
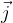 ha la stessa direzione dell'asse y ed il vettore
ha la stessa direzione dell'asse y ed il vettore 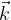 ha la stessa direzione dell'asse z, come si evince da Figura1 e Figura2.
ha la stessa direzione dell'asse z, come si evince da Figura1 e Figura2.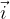 e
e 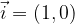
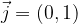
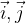 e
e 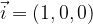
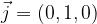
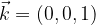
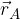 sono uguali alle coordinate del punto A.
sono uguali alle coordinate del punto A.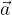 di componenti
di componenti 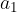 e
e 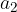 ed un vettore
ed un vettore 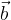 di componenti
di componenti 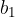 e
e 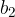 .
.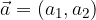
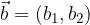
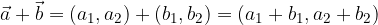
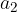 per uno scalare, basta moltiplicare il numero stesso per ciascuna delle componenti del vettore.
per uno scalare, basta moltiplicare il numero stesso per ciascuna delle componenti del vettore.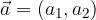
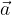 :
: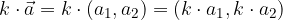
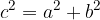
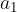 ed
ed 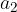 come in Figura3.
come in Figura3.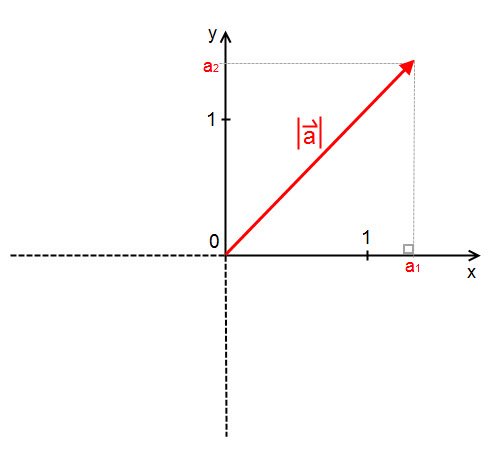
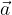 , note le componenti
, note le componenti 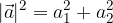
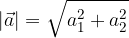
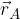 e
e 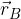 . Le componenti del vettore
. Le componenti del vettore 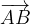 si calcolano come:
si calcolano come: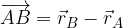
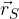 associato al punto S è uguale alla metà della somma dei vettori locali
associato al punto S è uguale alla metà della somma dei vettori locali 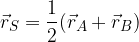
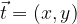
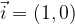
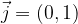
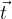 di componenti (x,y) si esprime come:
di componenti (x,y) si esprime come: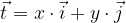
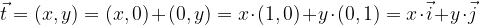
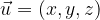
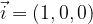
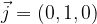
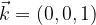
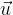 di componenti (x,y,z) si esprime come:
di componenti (x,y,z) si esprime come: