Il Teorema di Pitagora è un importante teorema che mette in relazione i lati di un triangolo rettangolo.
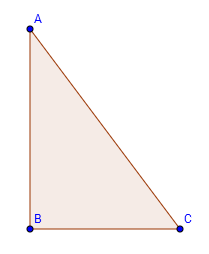
Triangolo rettangolo 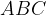
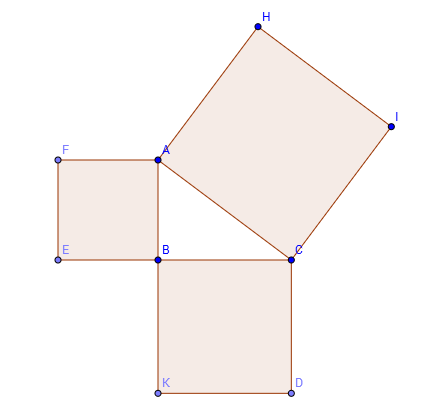
la somma dei quadrati costruiti sui cateti è equivalente al quadrato costruito sull'ipotenusa.
Ovvero: il quadrato costruito sul lato AB sommato al quadrato sul lato BC ha area equivalente al quadrato costruito sul lato AC. In formule:
Se in un triangolo la somma dei quadrati dei due lati minori è equivalente al quadrato del lato maggiore, allora il triangolo è rettangolo con cateti i due lati minori.
Spieghiamo tramite alcuni esempi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Nel caso di un'applicazione inversa del teorema di Pitagora.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dalla formula 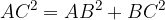 possiamo ricavare le formule inverse
possiamo ricavare le formule inverse
si applica ai triangoli rettangoli
è utile per ricavare un lato (cateto o ipotenusa) conoscendo gli altri due
è utile per verificare se un triangolo è rettangolo, conoscendo le misure dei tre lati
afferma che in ogni triangolo rettangolo la somma dei quadrati costruiti sui due cateti è equivalente al quadrato costruito sull'ipotenusa
Dimostrazioni
Il Teorema di Pitagora ha molte dimostrazioni celebri. Lo scienziato americano Elisha Scott Loomis, nel suo libro The Pythagorean Proposition pubblicato nel 1927, classificò ben 371 differenti dimostrazioni. La maggior parte delle dimostrazioni si basa sulla scomposizione in figure equivalenti e ne proponiamo alcune negli esercizi.
Riportiamo invece per esteso la dimostrazione classica di Euclide, con la quale si conclude il Primo Libro degli Elementi, e un'elegante e molto interessante dimostrazione trovata nel 1876 dal futuro XX Presidente degli Stati Uniti d'America, James Abraham Garfield.
La dimostrazione di Euclide
La dimostrazione di Euclide in sé è molto semplice, anche se negli Elementi vi è una lunga premessa per dimostrare che i quadrati sui cateti e l'ipotenusa possono effettivamente esistere ed essere costruiti.
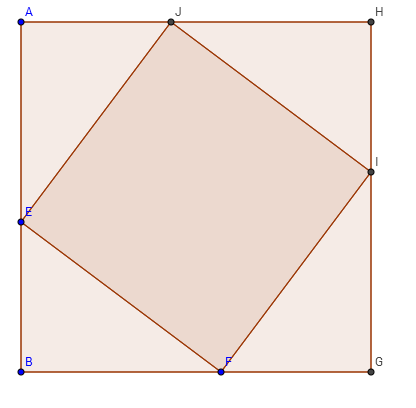
L'area dei due quadrati costruiti sui cateti è equivalente all'area del quadrato di lato la somma dei cateti meno quattro volte l'area del triangolo di partenza
L'area del quadrato costruito sull'ipotenusa è equivalente all'area del quadrato di lato la somma dei cateti meno quattro volte l'area del triangolo di partenza
Come si vede immediatamente dalla figura e si può dimostrare anche formalmente, possiamo sottrarre, in due modi diversi, quattro volte l'area del triangolo di partenza al quadrato di lato la somma dei cateti, ottenendo in un caso i due quadrati di lato rispettivamente il cateto minore e il cateto maggiore, e nell'altro caso il quadrato costruito sull'ipotenusa.
E' quindi verificata l'uguaglianza del Teorema di Pitagora.
La dimostrazione di Garfield
James Abraham Garfield fu insegnante in un college, poi avvocato, e combatté nelle truppe dell’Unione durante la Guerra Civile; nel 1876 trovò una nuova dimostrazione del teorema di Pitagora e commentò così la scoperta: Questo è qualcosa su cui i due rami del Parlamento potranno essere d’accordo. Pochi anni dopo fu candidato ed eletto XX presidente degli Stati Uniti d'America, ma morì poco tempo dopo prematuramente.
Ecco la sua dimostrazione. Si noterà che la figura utilizzata è ricavabile come metà del secondo quadrato della dimostrazione di Euclide.
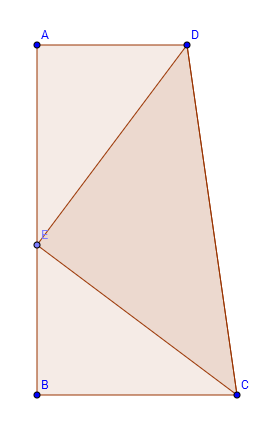
La dimostrazione di Garfield
mentre l'area del trapezio 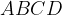 vale
vale
dove la prima delle somme 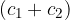 rappresenta la somma delle basi del trapezio, mentre la seconda rappresenta la misura dell'altezza.
rappresenta la somma delle basi del trapezio, mentre la seconda rappresenta la misura dell'altezza.
Pareggiando le aree, poichè l'area del trapezio è pari alla somma delle aree dei tre diversi triangoli in cui è scomponibile, si ottiene:
da cui si ricava facilmente
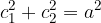 .
.
Notizie storiche e filosofiche
Tra le dimostrazioni più classiche del Teorema di Pitagora, ricordiamo quella del matematico persiano Nasir ad-Din at-Tusi (Tus, 1202 - Baghdad, 1274) riportata in un' edizione araba degli Elementi di Euclide datata 1594. Si tratta in realtà della dimostrazione classica del Primo Teorema di Euclide, applicata alle due parti del triangolo.
Un'altra dimostrazione classica proveniente dal medioevo islamico è quella di Abu-l-Wafa Muhammad al-Buzjani (~ 970), detto al-Muhandis (l'architetto). Tale dimostrazione, interessante per il fatto che il motivo ornamentale che se ne produce si trova in molte architetture islamiche, viene presentata da Abu-l-Wafa come caso particolare in un celebre trattato sulla triplicazione del quadrato, ma divenne celebre in Europa soltanto nel XIX secolo grazie a un agente di cambio, Henry Perigal, che la illustrò estesamente intorno al 1840 e al quale viene generalmente attribuita.
Interessante come il teorema di Pitagora, e in particolare la terna pitagorica 3-4-5, venga proposto da Abu-l-Wafa come metodo tradizionalmente noto agli artigiani della sua epoca per la costruzione di un attrezzo di lavoro indispensabile: la squadra. Leggiamo nell'Enciclopedia Treccani: "Tra tali metodi, quello che egli attribuisce agli artigiani e che sembra essere stato in uso fin dall'Antichità, si basa sul teorema di Pitagora (si traccia con il compasso un segmento lungo 3 unità su un lato della squadra, uno lungo 4 sull'altro lato e si verifica che la retta che unisce gli estremi sia lunga 5); ritroveremo questo metodo di verifica della perpendicolarità basato sul calcolo in tutti i trattati di geometria pratica" (Hélène Bellosta, "La civilta islamica: antiche e nuove tradizioni in matematica. Geometria pratica", in Storia della Scienza, Enciclopedia Treccani, 2002)
Glossario
cateto: ciascun lato del triangolo rettangolo adiacente all'angolo retto
ipotenusa: il lato del triangolo rettangolo opposto all'angolo retto
terna pitagorica: una terna di numeri interi che soddisfino la relazione del Teorema di Pitagora, ovvero tali che il quadrato del maggiore fra i tre numeri sia pari alla somma dei quadrati degli altri due. Le più note e utilizzate terne pitagoriche sono 3-4-5 e 5-12-13 .





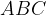
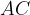 e cateti
e cateti 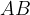 e
e 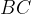 , si dimostra il seguente teorema:
, si dimostra il seguente teorema: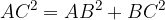
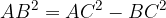
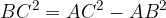
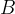 , e costruiamo un quadrato di lato
, e costruiamo un quadrato di lato  , cioè pari alla somma dei due cateti.
, cioè pari alla somma dei due cateti.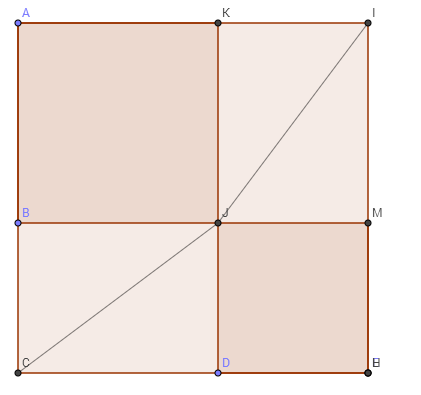

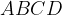 avente le basi
avente le basi 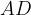 e
e 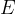 tale che
tale che 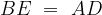 e
e 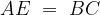 .
.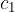 la misura del cateto minore
la misura del cateto minore 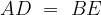 e
e 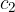 la misura del cateto maggiore
la misura del cateto maggiore 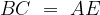 .
.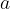 la misura dell'ipotenusa del nostro triangolo, rappresentata dai segmenti
la misura dell'ipotenusa del nostro triangolo, rappresentata dai segmenti 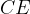 ee
ee 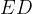 .
.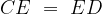 in quanto i triangoli
in quanto i triangoli 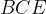 e
e 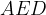 risultano congruenti per il primo criterio di congruenza dei triangoli (i cateti sono a due a due congruenti per costruzione, e l'angolo compreso è di 90°).
risultano congruenti per il primo criterio di congruenza dei triangoli (i cateti sono a due a due congruenti per costruzione, e l'angolo compreso è di 90°).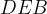 è di 90° in quanto gli angoli
è di 90° in quanto gli angoli 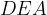 e
e 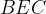 sono complementari.
sono complementari.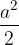 .
.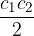
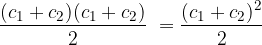
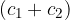 rappresenta la somma delle basi del trapezio, mentre la seconda rappresenta la misura dell'altezza.
rappresenta la somma delle basi del trapezio, mentre la seconda rappresenta la misura dell'altezza.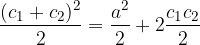
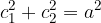 .
.


