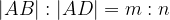Suddivisione di un segmento in 2, 4, 8,... 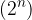 parti uguali
parti uguali
Costruiamo geometricamente la suddivisione di un segmento in 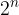 parti uguali.
parti uguali.
Prima di tutto, rappresentiamo il segmento 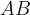 con un disegno:
con un disegno:
Per dividere il segmento 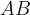 in due parti uguali basta costruire il suo punto medio:
in due parti uguali basta costruire il suo punto medio:
Con riferimento all'immagine qui sopra, si avrà:
ovvero il segmento 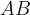 è stato suddiviso in due parti di uguale lunghezza.
è stato suddiviso in due parti di uguale lunghezza.
Il segmento 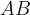 risulta quindi diviso in quattro parti della stessa lunghezza, pari a un quarto della misura del segmento.
risulta quindi diviso in quattro parti della stessa lunghezza, pari a un quarto della misura del segmento.
Si ripete la procedura descritta nei passi 1 e 2, costruendo ogni volta il punto medio di ogni segmento che compone la suddivisione precedente: i segmenti totali risulteranno ogni volta raddoppiati di numero, e la loro lunghezza sarà la metà della lunghezza delle parti ottenute al passo immediatamente precedente.
Questo procedimento viene utilizzato in analisi numerica quando si applica il metodo della bisezione per la ricerca degli zeri di una funzione, ad esempio è molto usata nel caso dei polinomi.
Suddivisione di un segmento in n parti uguali
Supponiamo di avere già disegnato il nostro segmento 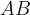 :
:
A partire dall'estremo A disegniamo una semiretta obliqua h
Prendiamo un compasso con apertura a fissata a piacere
Puntando il compasso in 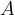 individuiamo sulla semiretta un segmento di lunghezza a
individuiamo sulla semiretta un segmento di lunghezza a
Chiamiamo 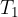 il secondo estremo del segmento trovato
il secondo estremo del segmento trovato
Puntando il compasso in 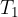 disegniamo sulla semiretta un nuovo segmento di lunghezza a: chiamiamo
disegniamo sulla semiretta un nuovo segmento di lunghezza a: chiamiamo 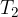 il secondo estremo
il secondo estremo
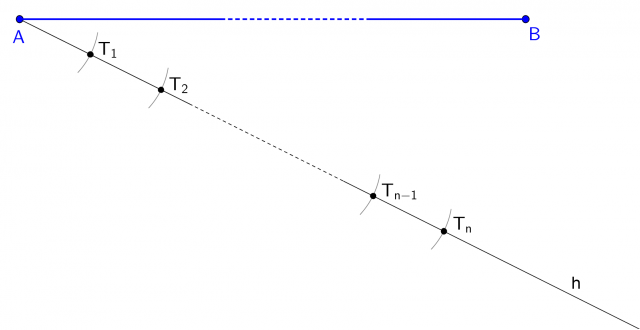
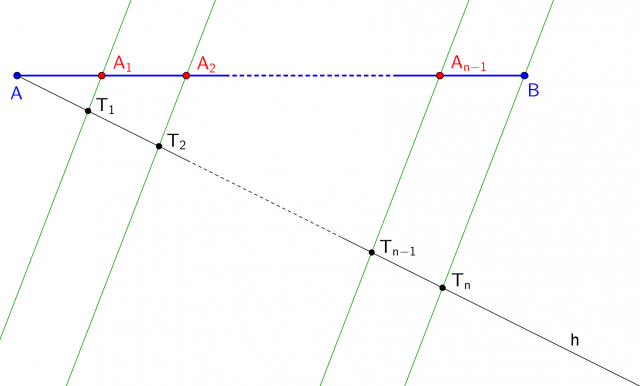
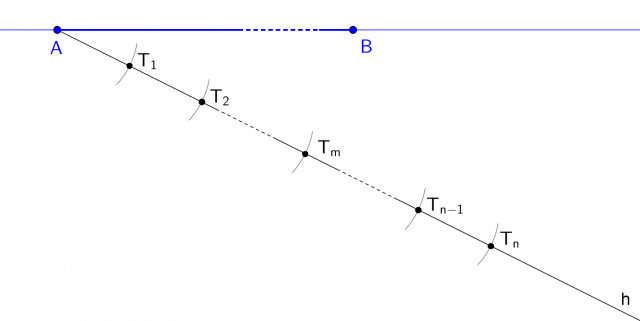
Ripetendo n volte l'operazione, individuiamo n segmenti di lunghezza a; l'ultimo estremo trovato sarà 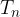 :
:
Disegniamo la retta passante per 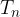 e
e 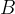 .
.
I punti così costruiti dividono il segmento 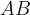 in n parti di uguale lunghezza:
in n parti di uguale lunghezza:
Questo procedimento può essere usato anche per trovare una parte frazionaria di un segmento, come mostrato nel seguente esempio:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dividere un segmento in un rapporto m:n
Poniamo di aver disegnato il nostro segmento 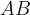 :
:
A partire dall'estremo A disegniamo una semiretta obliqua h
Prendiamo un compasso con apertura a fissata a piacere
Puntando il compasso in 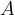 individuiamo sulla semiretta un segmento di lunghezza a
individuiamo sulla semiretta un segmento di lunghezza a
Chiamiamo 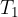 il secondo estremo del segmento trovato
il secondo estremo del segmento trovato
Puntando il compasso in 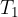 disegniamo sulla semiretta un nuovo segmento di lunghezza a: chiamiamo
disegniamo sulla semiretta un nuovo segmento di lunghezza a: chiamiamo 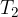 il secondo estremo
il secondo estremo
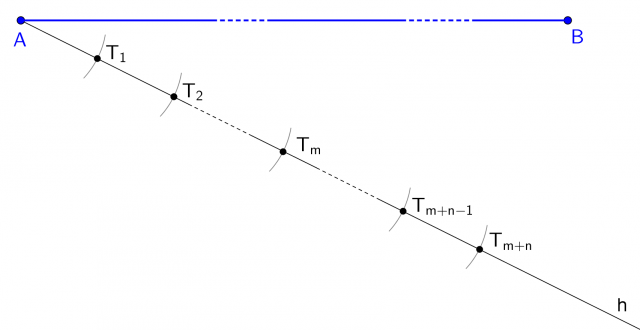
Ripetendo m+n volte l'operazione, individuiamo m+n segmenti di lunghezza a; l'ultimo estremo trovato sarà 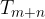 :
:
Tracciamo la retta che congiunge 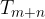 e
e 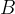 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Estendere un segmento nel rapporto m:n
Consideriamo qui la costruzione nel caso in cui
Supponiamo di aver già disegnato il segmento 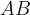 :
:
Tracciamo la retta che contiene il segmento 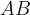 .
.
A partire dall'estremo A disegniamo una semiretta obliqua h
Prendiamo un compasso con apertura a fissata a piacere
Puntando il compasso in 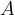 individuiamo sulla semiretta un segmento di lunghezza a
individuiamo sulla semiretta un segmento di lunghezza a
Chiamiamo 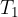 il secondo estremo del segmento trovato
il secondo estremo del segmento trovato
Puntando il compasso in 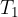 disegniamo sulla semiretta un nuovo segmento di lunghezza a: chiamiamo
disegniamo sulla semiretta un nuovo segmento di lunghezza a: chiamiamo 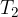 il secondo estremo
il secondo estremo
Ripetendo n volte l'operazione, individuiamo n segmenti di lunghezza a; l'ultimo estremo trovato sarà 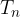 :
:
Tracciamo la retta che congiunge i punti 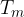 e
e 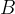 .
.
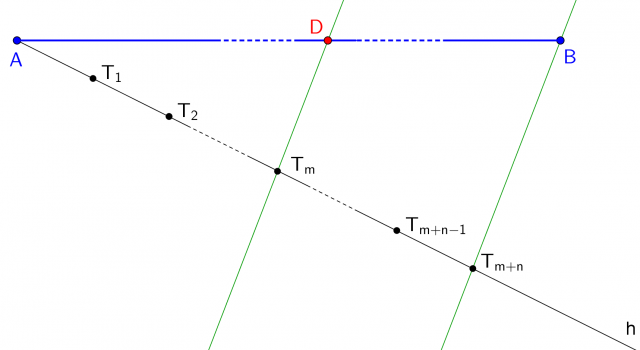
Per costruzione, possiamo dire che 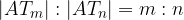 , quindi avremo anche
, quindi avremo anche 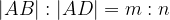
In conclusione, il punto D estende il segmento 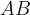 nella proporzione m:n.
nella proporzione m:n.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »


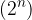 parti uguali
parti uguali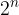 parti uguali.
parti uguali.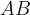 con un disegno:
con un disegno:

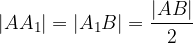
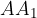 e chiamiamolo
e chiamiamolo 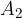 .
.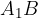 e chiamiamolo
e chiamiamolo 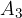 :
:
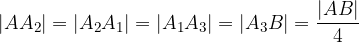
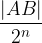 .
.
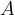 individuiamo sulla semiretta un segmento di lunghezza a
individuiamo sulla semiretta un segmento di lunghezza a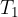 il secondo estremo del segmento trovato
il secondo estremo del segmento trovato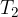 il secondo estremo
il secondo estremo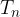 :
:
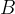 .
. tracciamo la retta parallela a
tracciamo la retta parallela a  . Le rette costruite intersecheranno il segmento
. Le rette costruite intersecheranno il segmento  .
.
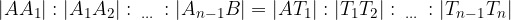
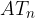 sono congruenti, anche il segmento
sono congruenti, anche il segmento  .
.
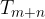 :
:
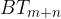 e passante per il punto
e passante per il punto 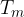 . Questa nuova retta taglierà il segmento
. Questa nuova retta taglierà il segmento 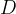 :
:
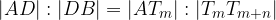
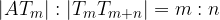 , possiamo quindi concludere che
, possiamo quindi concludere che 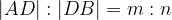 e quindi il segmento
e quindi il segmento 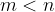

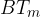 . Questa nuova retta incontrerà la retta contenente
. Questa nuova retta incontrerà la retta contenente 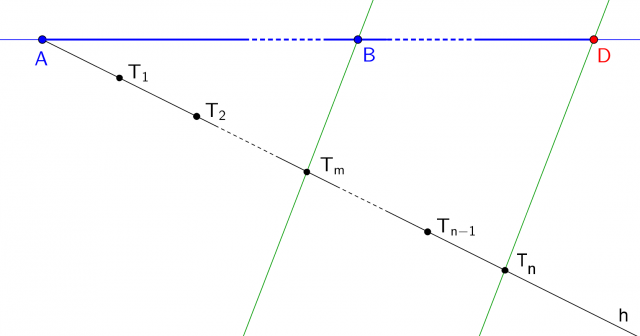
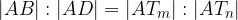
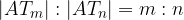 , quindi avremo anche
, quindi avremo anche