Una successione reale molto importante è quella aritmetica, in quanto è molto intuitiva e facile da studiare.
Una successione reale si dice aritmetica di punto iniziale a e ragione d se è della forma:
Intuitivamente la successione aritmetica parte da un numero a e si "muove" di n "passi" di lunghezza d sulla retta reale.
Successione aritmetica di ragione d e punto iniziale a
Prendendo due termini 
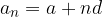
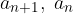consecutivi sottraiamo il secondo al primo: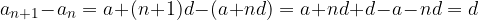
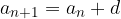
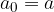
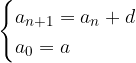
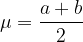
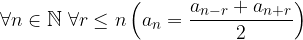
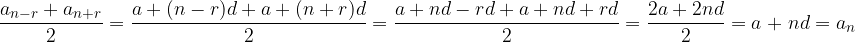
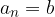Riscriviamo l' uguaglianza precedente:
In più sappiamo che il primo termine è proprio il punto iniziale:
Una successione aritmetica di ragione d e punto iniziale a si può presentare in maniera ricorsiva:
Ricordiamo la definizione di media aritmetica:
Dati due numeri reali a e b, la loro media aritmetica è il numero reale:
Un'importante proprietà della successione aritmetica si può esprimere tramite media aritmetica.
Ogni termine è media aritmetica di altri due termini che sono alla medesima distanza da esso
Dimostrazione:
Una notevole applicazione della successione aritmetica è quella di suddividere in sotto-intervalli uguali un intervallo limitato [a , b]: per far ciò è sufficiente decidere in quante parti si vuol dividere l' intervallo e calcolare gli estremi dei nuovi sotto-intervalli.
Suddivisione a passo costante
Dato un intervallo limitato [a , b], gli estremi dei suoi n sotto-intervalli di ugual lunghezza sono determinati dalla successione aritmetica finita:
è il punto iniziale
è il punto finale
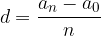: si chiama passo della suddivisione (in questo caso è costante)
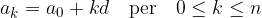sono i nuovi estremi dei sotto-intervalli
I sotto-intervalli saranno della forma 
Vediamo un esempio.
