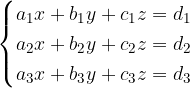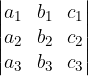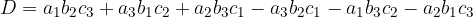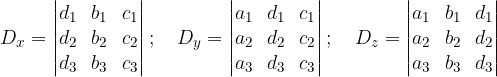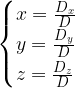Per risolvere un sistema si cerca di trasformarlo, mediante l'applicazione dei principi d'equivalenza delle equazioni, in sistemi equivalenti via via più semplici, fino ad ottenere un sistema che ci permetta di determinare in modo immediato l'insieme delle soluzioni.
Il metodo di sostituzione
Per risolvere un sistema di due equazioni lineari in due incognite col metodo di sostituzione si procede nel seguente modo:
si riduce il sistema in forma normale;
si risolve una delle due equazioni (quella che appare più semplice) rispetto a una delle incognite;
si sostituisce l'espressione trovata, nell'altra equazione, la quale diventa un'equazione ad una sola incognita, si trova così facilmente il valore della seconda incognita;
si sostituisce tale valore nella prima equazione considerata, determinando così anche il valore dell'altra incognita.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il metodo di confronto
Generalmente il metodo di confronto si usa quando le due equazioni sono già esplicitate rispetto alla stessa variabile; se lo si vuole utilizzare a prescindere, la prima operazione da fare è proprio quella di scrivere entrambe le equazioni in funzione della stessa variabile. Dopodiché si confrontano, cioè si eguagliano, le due espressioni ottenute. Si ha perciò un'equazione in una sola incognita e la si risolve, ottenendo appunto il valore dell'incognita. Sostituendo tale risultato in una delle due equazioni (quella che appare più semplice) si va a trovare il valore dell'altra incognita.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il metodo di riduzione (o di addizione e sottrazione)
Questo metodo si basa sul principio di riduzione secondo il quale se ad un'equazione del sistema si sostituisce quella che si ottiene sommando o sottraendo ad essa, membro a membro, un'altra equazione del sistema, si ottiene un sistema equivalente a quello dato.
Tramite questo metodo, addizionando o sottraendo i termini delle equazioni si fa in modo di eliminare subito un'incognita, così da ottenere facilmente l'altra.
Più precisamente, se i coefficienti dell'incognita da eliminare, in entrambe le equazioni date, sono:
uguali, allora si sottraggono membro a membro le due equazioni;
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
opposti, allora si sommano membro a membro le due equazioni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Se non sono nè uguali, nè opposti, si moltiplicano le equazioni per opportune costanti non nulle, in modo che i coefficienti delle incognite da eliminare divengano uguali o opposti, così da poterli sottrarli o addizionarli tra loro.
Eliminata un'incognita, si risolve facilmente l'equazione, ottenendo l'altra incognita.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La regola di Cramer
Dalla generalizzazione del metodo di riduzione, si arriva alla regola di Cramer.
Considerando un generico sistema lineare di due equazioni, con due incognite, ridotto a forma normale
dove 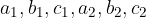 rappresentano numeri reali
rappresentano numeri reali
la regola di Cramer ci permetterà di stabilire la coppia soluzione di tale sistema costruendo e calcolando tre determinanti:
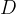 il determinante della matrice del sistema, che si ottiene scrivendo i coefficienti della x e della y nelle due equazioni, incolonnati in una tabella. Il valore del determinante è la somma del prodotto degli elementi sulla diagonale principale con il prodotto, cambiato di segno, degli elementi sulla diagonale secondaria.
il determinante della matrice del sistema, che si ottiene scrivendo i coefficienti della x e della y nelle due equazioni, incolonnati in una tabella. Il valore del determinante è la somma del prodotto degli elementi sulla diagonale principale con il prodotto, cambiato di segno, degli elementi sulla diagonale secondaria.
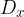 il determinante della matrice ottenuta sostituendo in D agli elementi della prima colonna i termini noti.
il determinante della matrice ottenuta sostituendo in D agli elementi della prima colonna i termini noti.
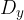 il determinante della matrice ottenuta sostituendo in D agli elementi della seconda colonna i termini noti.
il determinante della matrice ottenuta sostituendo in D agli elementi della seconda colonna i termini noti.
Con queste convenzione, è possibile affermare che:
Sistemi determinati
se 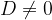 il sistema è determinato e la sua soluzione è
il sistema è determinato e la sua soluzione è
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sistemi indeterminati e impossibili
se 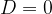 si possono verificare due casi:
si possono verificare due casi:
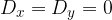 , il sistema è indeterminato, ciò significa che ogni coppia di numeri reali che verifica un’equazione, verifica anche l’altra;
, il sistema è indeterminato, ciò significa che ogni coppia di numeri reali che verifica un’equazione, verifica anche l’altra;
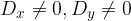 , il sistema è impossibile, ciò significa che non esiste alcuna coppia che soddisfa entrambi le equazioni.
, il sistema è impossibile, ciò significa che non esiste alcuna coppia che soddisfa entrambi le equazioni.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
OSSERVAZIONE: Per stabilire se un sistema, il cui determinante è zero, è impossibile oppure indeterminato, non è necessario calcolare i determinanti di entrambe le incognite, come fatto negli esempi precedenti, ma è sufficiente calcolare il determinante di una sola incognita.
Infatti, si può dimostrare che, se 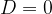 allora i determinanti delle incognite o sono tutti nulli (caso in cui il sistema risulta indeterminato) oppure sono tutti diversi da zero (caso in cui il sistema risulta impossibile).
allora i determinanti delle incognite o sono tutti nulli (caso in cui il sistema risulta indeterminato) oppure sono tutti diversi da zero (caso in cui il sistema risulta impossibile).
Sistemi di tre equazioni in tre incognite
La regola di Cramer, permette anche la risoluzione dei sistemi di tre equazioni con tre incognite.
Per poterla applicare a tali sistemi, occorre però estendere opportunamente il concetto di determinante.
Consideriamo un generico sistema di tre equazioni in tre incognite in forma normale:
si chiama determinante del sistema e si indica con il seguente simbolo
il numero 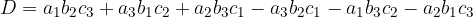
ottenuto scrivendo i coefficienti delle tre incognite nelle tre equazioni opportunamente incolonnati.
Più precisamente, si ricorre alla regola di Sarrus, che prevede di riscrivere a destra della terza colonna, la prima e la seconda; poi di moltiplicare gli elementi che si trovano sulle diagonali e di sommare i prodotti ottenuti, prendendo con il loro segno i prodotti degli elementi delle diagonali principali e con il segno cambiato i prodotti degli elementi sulle diagonali secondarie.
Analogamente ai sistemi di due equazioni in due incognite, si definisce determinante di un'incognita quel determinante che si ottiene dal determinante del sistema sostituendo, al posto dei coefficienti dell'incognita considerata, i termini noti della corrispondente equazione.
Anche i valori numerici di tali determinanti possono essere calcolati ricorrendo alla regola di Sarrus.
se 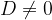 il sistema è determinato e la sua soluzione è
il sistema è determinato e la sua soluzione è
se 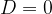 il sistema può risultare impossibile oppure indeterminato. Applicando il metodo di sostituzione o di eliminazione, si potrà stabilire quale dei due casi si presenti.
il sistema può risultare impossibile oppure indeterminato. Applicando il metodo di sostituzione o di eliminazione, si potrà stabilire quale dei due casi si presenti.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sistemi a coefficienti letterali
Se un sistema lineare presenta coefficienti letterali in almeno una sua equazione, è possibile risolverlo con uno dei metodi già disquisiti, l'unica differenza è che occorre discutere il sistema, analizzare cioè per quali valori dei parametri esso è determinato o indeterminato oppure impossibile.
Sistemi frazionari
I sistemi frazionari sono quei sistemi in cui almeno in una delle equazioni che lo compongono compare l’incognita al denominatore. Si risolvono con i metodi già visti, previa definizione del dominio.
Dove per dominio del sistema fratto, si intende l’insieme delle coppie ordinate che rendono diversi da zero i denominatori presenti nelle equazioni.





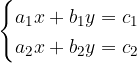
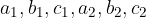 rappresentano numeri reali
rappresentano numeri reali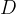 il determinante della matrice del sistema, che si ottiene scrivendo i coefficienti della x e della y nelle due equazioni, incolonnati in una tabella. Il valore del determinante è la somma del prodotto degli elementi sulla diagonale principale con il prodotto, cambiato di segno, degli elementi sulla diagonale secondaria.
il determinante della matrice del sistema, che si ottiene scrivendo i coefficienti della x e della y nelle due equazioni, incolonnati in una tabella. Il valore del determinante è la somma del prodotto degli elementi sulla diagonale principale con il prodotto, cambiato di segno, degli elementi sulla diagonale secondaria.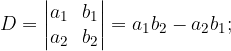
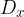 il determinante della matrice ottenuta sostituendo in D agli elementi della prima colonna i termini noti.
il determinante della matrice ottenuta sostituendo in D agli elementi della prima colonna i termini noti.
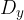 il determinante della matrice ottenuta sostituendo in D agli elementi della seconda colonna i termini noti.
il determinante della matrice ottenuta sostituendo in D agli elementi della seconda colonna i termini noti.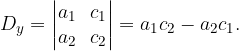
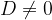 il sistema è determinato e la sua soluzione è
il sistema è determinato e la sua soluzione è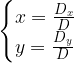
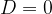 si possono verificare due casi:
si possono verificare due casi: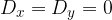 , il sistema è indeterminato, ciò significa che ogni coppia di numeri reali che verifica un’equazione, verifica anche l’altra;
, il sistema è indeterminato, ciò significa che ogni coppia di numeri reali che verifica un’equazione, verifica anche l’altra;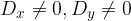 , il sistema è impossibile, ciò significa che non esiste alcuna coppia che soddisfa entrambi le equazioni.
, il sistema è impossibile, ciò significa che non esiste alcuna coppia che soddisfa entrambi le equazioni.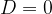 allora i determinanti delle incognite o sono tutti nulli (caso in cui il sistema risulta indeterminato) oppure sono tutti diversi da zero (caso in cui il sistema risulta impossibile).
allora i determinanti delle incognite o sono tutti nulli (caso in cui il sistema risulta indeterminato) oppure sono tutti diversi da zero (caso in cui il sistema risulta impossibile).