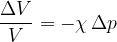Ogni corpo è costituito da particelle, che possono essere atomi, molecole o ioni, tenute insieme da interazioni di natura elettrica che a seconda dell'intensità ne determinano lo stato di aggregazione. La materia si può trovare in natura in diversi stati, i cui principali per il nostro studio sono:
solido: è lo stato più stabile, grazie alle forti interazioni elettriche. Le particelle che lo compongono sono disposte in maniera ordinata e hanno una posizione fissa. Questa caratteristica conferisce al solido un volume e una forma propri.
liquido: le particelle dei liquidi sono soggette a interazioni meno forti di quelle dei solidi. Sono, perciò, libere di muoversi, ma mantenendo un volume proprio.
gassoso: le forze interparticellare sono molto basse, perciò i gas non hanno né forma né volume proprio e sono comprimibili.
Quando agisce una forza esterna su un corpo, essa lo deforma. Le distanze tra molecole aumentano o diminuiscono - a seconda della direzione della forza esterna.
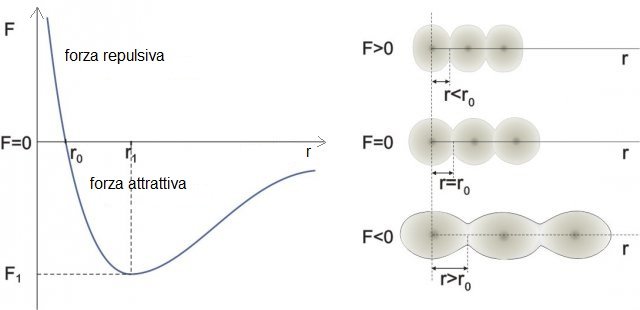
Figura 1: La dipendenza della distanza tra le particelle in funzione di una forza esterna
Dalla figura 1 possiamo notare alcune cose:
quando la forza esterna è maggiore di zero, il corpo si accorcia e le molecole distano 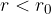 e ci sono delle forze repulsive che si oppongono alla forza esterna;
e ci sono delle forze repulsive che si oppongono alla forza esterna;
quando la forza esterna invece è negativa, il corpo si allunga e le molecole distano 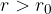 e ci sono delle forze di attrazione tra le molecole che si oppone all'allungamento;
e ci sono delle forze di attrazione tra le molecole che si oppone all'allungamento;
quando la forza invece è nulla, il corpo non è deformato e le molecole distano tra loro 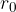 .
.
In questo capitolo ci occuperemo dei solidi, in particolare dei solidi su cui agiscono degli sforzi.
Sforzi
Un corpo solido, come abbiamo detto sopra, può trovarsi in equilibrio pur essendo sottosto a forze, venendo così deformato. Il rapporto tra il modulo F della forza applicata e l'area A del corpo su cui agisce la forza, è chiamato sforzo:
Supponendo che il corpo sia vincolato in modo che l'applicazione di una forza non ne modifichi lo stato di quiete, a seconda della direzione della forza rispetto alla superficie di applicazione abbiamo vari tipi di sforzi:
Vedremo in dettaglio solamente i primi due tipi.
Sforzi di trazione
Uno sforzo di trazione si ha quando la forza viene applicata perpendicolarmente ad una superficie di un solido, in modo da tendere ad allungarlo:
In figura c'è una figura che rappresenta un esempio di sforzo di trazione.
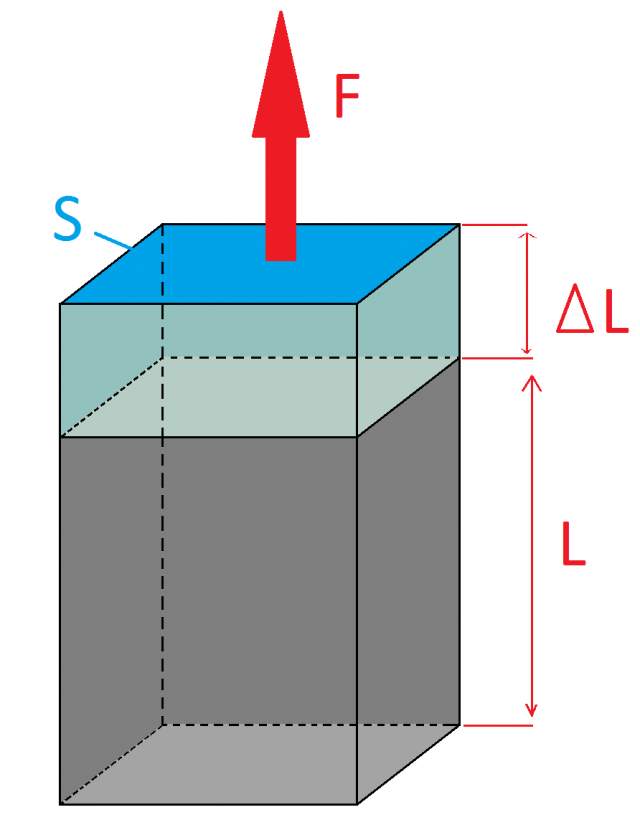
Figura 4 : Sforzo di trazione
Sforzi di compressione
Uno sforzo di compressione si ha quando la forza viene sempre applicata perpendicolarmente ad una superficie di un solido, in modo, però, da tendere ad accorciarlo:
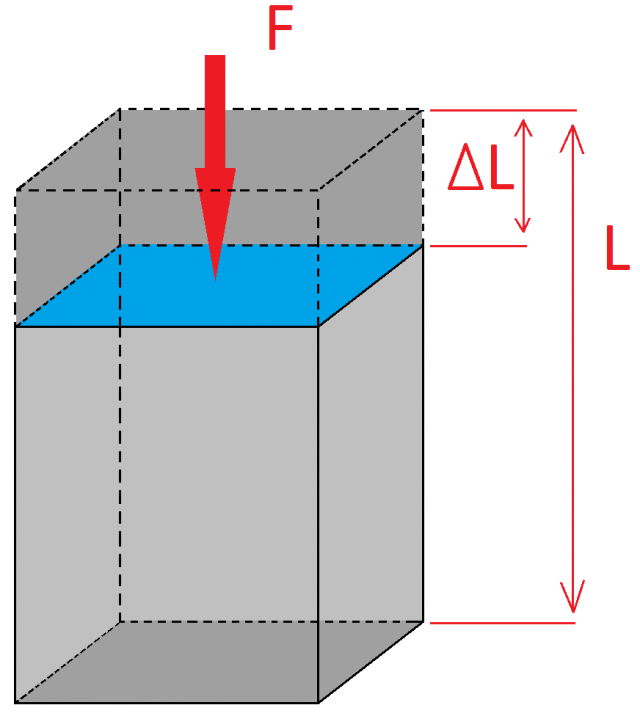
Figura 5 : Sforzo di compressione
Solidi in trazione
Immaginiamo un corpo esteso su cui è applicata una trazione (vedi figura 4):
Figura 4 : La sollecitazione di trazione provoca lo stelo esteso
Consideriamo una trazione 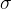 su una barra di lunghezza l che causa un allungamento x. È possibile definire l'allungamento relativo
su una barra di lunghezza l che causa un allungamento x. È possibile definire l'allungamento relativo  :
:
L'allungamento relativo non ha un'unità dimisura, dal momento che le unità numeratore e denominatore sono le stesse e si semplificano.
Per dei relativamente piccoli sforzi di trazione, si può applica una relazione lineare tra trazione e l'allungamento relativo:
Dove E rappresenta il modulo di elasticità . Esso dipende solo dal tipo di materiale selezionato e non dalla forma del corpo . La (1) è un altro modo di scrivere la già nota legge di hooke.
Dalla (1) possiamo ricavare E e possiamo capire come misurarlo:
Esso è quindi misurato in 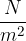 .
.
La figura 2 mostra la dipendenza della trazione dall'allungamento relativo.
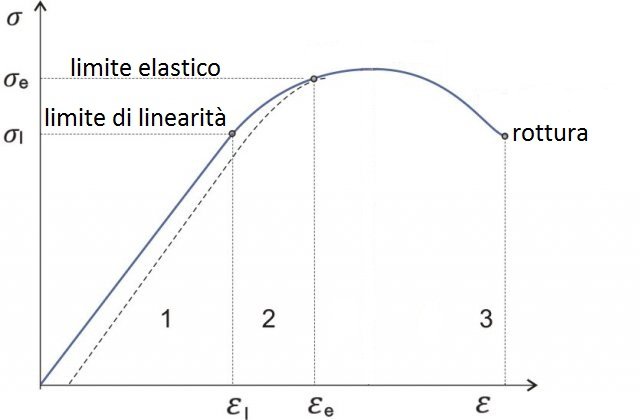
Figura 2: la dipendenza della tensione e allungamento relativo
Il grafico della Figura 2 è suddiviso in tre sezioni:
deformazione elastica lineare
Nella prima parte tra le due grandezze c'è una dipendenza lineare fino a un punto limite 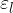 . In questa fase il corpo rispetta la (1).
. In questa fase il corpo rispetta la (1).
deformazione elastica non lineare
Dopo aver superato il limite lineare 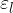 , il corpo comincia ad essere allungato non più in maniera lineare.
, il corpo comincia ad essere allungato non più in maniera lineare.
deformazione plastica e rottura
Superando il limite lineare 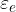 , il corpo comincia ad essere deformato irrimediabilmente e se superiamo il limite di deformazione, il corpo si romperà.
, il corpo comincia ad essere deformato irrimediabilmente e se superiamo il limite di deformazione, il corpo si romperà.
Un solido sotto l'azione di uno sforzo di trazione si allunga. Entro il limite lineare, vale la seguente relazione::
dove E è il modulo di elasticità, che dipende solo dal materiale, e  l'allungamento relativo:
l'allungamento relativo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Solidi in compressione
Immaginamo un corpo su cui agisce uno sforzo di compressione (o pressione) p vedi figura 5 .
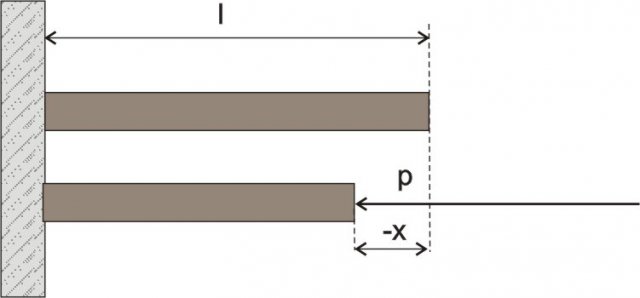
Figura 5:Uno sforzo di compressione provoca l'asta restringe
A causa della pressione , la lunghezza dell'asta è diminuita di x. Anche in questo caso si applica l'equazione (1), che abbiamo scritto nel paragrafo precedente, almeno fino a quando siamo in un tratto lineare:
Possiamo esplicitare  , come già sappiamo:
, come già sappiamo:
Che cosa succede se le forze di pressione che agiscono da tutte le direzioni sul corpo?
In questo caso, il corpo viene compresso e il volume V viene ridotto di 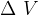 , come mostrato in Figura 6.
, come mostrato in Figura 6.
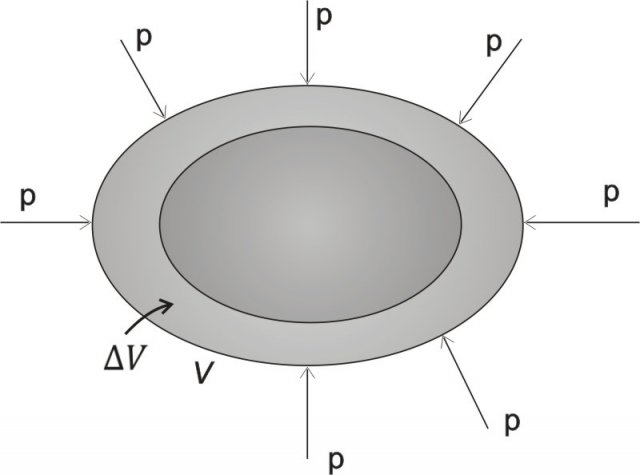
Figura 6 : Una compressione in tutte le direzioni provoca una riduzione del volume.
La relativa diminuzione di volume è proporzionale alle variazioni di sforzo di compressione nel corpo:
Il segno meno ( - ) è dovuto al fatto che un aumento di pressione determina una diminuzione di volume .
La costante di proporzionalità 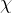 è la compressibilità della sostanza. L'unità è
è la compressibilità della sostanza. L'unità è 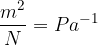 . L'inverso della compressibilità è detto modulo di comprimibilità:
. L'inverso della compressibilità è detto modulo di comprimibilità:
e si misura in 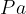 e al contrario della comprimibiltà in generale ha valori molto alti.
e al contrario della comprimibiltà in generale ha valori molto alti.
La variazione di volume è proporzionale allo sforzo di compressione che agisce su tutto il corpo:
il coefficiente di proporzionalità 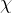 si chiama compressibilità della sostanza e dipende solo dal materiale scelto , e non dalla geometria del corpo.
si chiama compressibilità della sostanza e dipende solo dal materiale scelto , e non dalla geometria del corpo.
L'inverso della compressibilità è detto modulo di comprimibilità:
Il discorso della compressibilità può essere applicato tranquillamente anche ai liquidi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





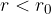 e ci sono delle forze repulsive che si oppongono alla forza esterna;
e ci sono delle forze repulsive che si oppongono alla forza esterna;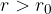 e ci sono delle forze di attrazione tra le molecole che si oppone all'allungamento;
e ci sono delle forze di attrazione tra le molecole che si oppone all'allungamento;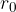 .
.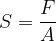
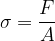

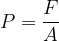


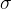 su una barra di lunghezza l che causa un allungamento x. È possibile definire l'allungamento relativo
su una barra di lunghezza l che causa un allungamento x. È possibile definire l'allungamento relativo  :
: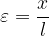

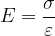
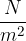 .
.
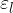 . In questa fase il corpo rispetta la (1).
. In questa fase il corpo rispetta la (1).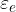 , il corpo comincia ad essere deformato irrimediabilmente e se superiamo il limite di deformazione, il corpo si romperà.
, il corpo comincia ad essere deformato irrimediabilmente e se superiamo il limite di deformazione, il corpo si romperà.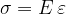
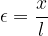

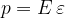
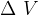 , come mostrato in Figura 6.
, come mostrato in Figura 6.

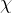 è la compressibilità della sostanza. L'unità è
è la compressibilità della sostanza. L'unità è 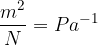 . L'inverso della compressibilità è detto modulo di comprimibilità:
. L'inverso della compressibilità è detto modulo di comprimibilità: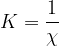
 e al contrario della comprimibiltà in generale ha valori molto alti.
e al contrario della comprimibiltà in generale ha valori molto alti.