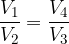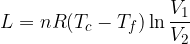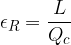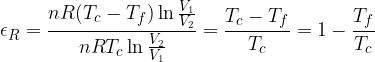Abbiamo visto che il primo principio della termodinamica stabilisce l'equivalenza tra calore scambiato e lavoro e che il calore assorbito o ceduto modifica l'energia interna del sistema.
Il primo principio ammette ad esempio che mettendo a contatto due corpi a differente temperatura il più caldo trasferisce calore al più freddo; non esclude però che si possa avere un percorso inverso (dal più freddo al più caldo)!
Nella realtà sappiamo che tale fenomeno non sarà mai osservabile. Ci sono ancora molti esempi di fenomeni osservabili sono in un verso, ad esempio: possiamo convertire totalmente il lavoro in calore (nel caso dell'attrito), ma non è possibile trasformare tutto il calore in lavoro. Da questi esempi deduciamo che in natura esistono delle trasformazioni irreversibili (cioè che avvengono in un solo verso).
Possiamo descrivere un ulteriore esempio di processo irreversibile prendendo spunto dall'osservazione di un corpo con una certa energia cinetica iniziale che scivola su un piano ruvido: il lavoro della forza di attrito si trasforma in calore che aumenta l'energia interna, questa energia interna però non può convertirsi spontaneamente in energia cinetica del blocco. Il Secondo Principio della Termodinamica ci riconduce proprio a queste osservazioni.
Ci sono due diversi enunciati del secondo principio, che però si rivelano del tutto equivalenti:
Enunciato di Kelvin-Planck
È impossibile realizzare una trasformazione ciclica il cui unico risultato sia la trasformazione in lavoro di tutto il calore assorbito da una sorgente omogenea
È impossibile realizzare una trasformazione il cui unico risultato sia quello di trasferire calore da un corpo più freddo a uno più caldo senza l'apporto di lavoro
Le macchine termiche
Per capire i due enunciati è necessario chiarire cosa sono le macchine termiche.
In poche parole sono schemi che rappresentano il funzionamento di quei motori (motori a combustione, motori diesel, macchine a vapore...) che impiegano energia termica per produrre lavoro.
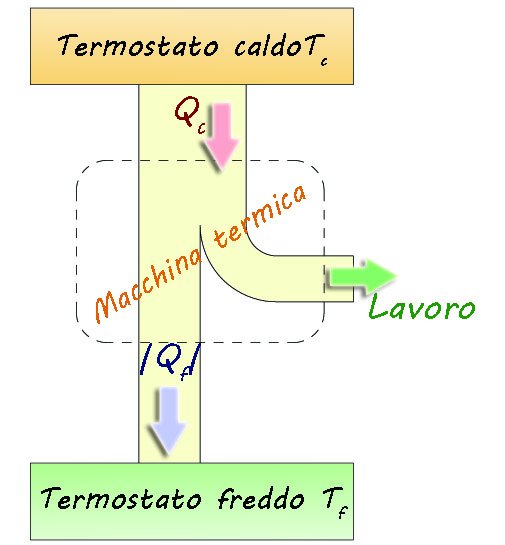
Schema di una macchina termica
Il valore assoluto è necessario perché 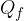 è un calore ceduto e quindi, secondo la convenzione dei segni, negativo, ma in questo caso ci interessa solo il modulo dei calori assorbiti e ceduti.
è un calore ceduto e quindi, secondo la convenzione dei segni, negativo, ma in questo caso ci interessa solo il modulo dei calori assorbiti e ceduti.
Il rendimento è definito come il rapporto tra lavoro e calore assorbito:
Vediamo che se volessimo ottenere il massimo rendimento (cioè pari a uno) il calore ceduto dovrebbe essere zero, cosicché tutto il calore assorbito dal termostato caldo viene trasformato in lavoro. Questo non è possibile ed è proprio quanto afferma l'enunciato di Kelvin.
Secondo principio della termodinamica - Enunciato di Kelvin-Planck
è impossibile una macchina termica che operi ciclicamente abbia come unico effetto quello di estrarre calore da un termostato e di compiere una quantità equivalente di lavoro.
Come è possibile far tornare il fluido al suo stato iniziale per completare il ciclo? Sappiamo che è possibile trasformare tutto il calore estratto da un unico termostato (o fonte di calore) in lavoro come accade ad esempio nell'espansione isoterma di un gas, ma una volta espanso il gas non torna alla sua configurazione iniziale a meno che non si ceda calore a un termostato a temperatura più bassa o non si compia lavoro su di esso. Si deve quindi "restituire" il lavoro.
In figura è schematizzata una macchina termica particolare, chiamata macchina frigorifera in cui si assorbe calore da un termostato freddo e lo si cede a u termostato caldo compiendo lavoro L:
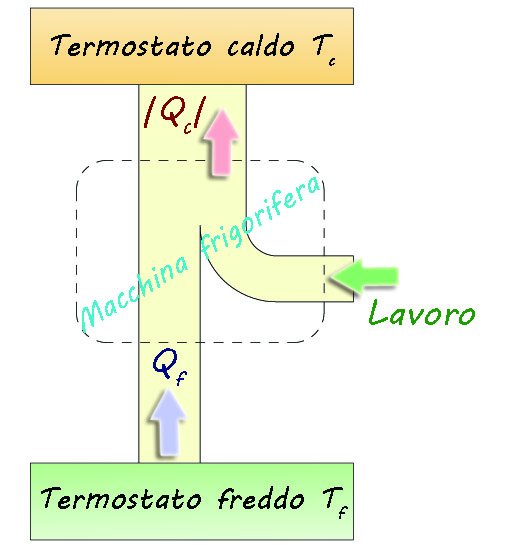
Schema di una macchina frigorifera
Una macchina frigorifera quindi serve a trasferire calore da un corpo freddo a un altro, (quindi a raffreddare) e secondo Clausius non è possibile senza compiere lavoro.
Secondo principio della termodinamica - Enunciato di Clausius
è impossibile costruire una macchina frigorifera, che operi ciclicamente, che abbia come unico effetto quello di trasferire calore da un corpo più freddo a uno più caldo.
Se ciò non fosse vero allora i condizionatori dell'aria funzionerebbero senza elettricità!
Per misurare l'efficienza di una macchina frigorifera introduciamo il coefficiente di effetto utile:
La Macchina di Carnot
La macchina di Carnot è una macchina reversibile ideale. Grazie a questo schema è stato calcolato il limite teorico del rendimento di una macchina termica in funzione delle temperature dei termostati.
I risultati ottenuti con la macchina di Carnot sono riassunti nel:
Non è possibile realizzare una macchina termica operante tra due termostati che abbia un rendimento maggiore di una macchina reversibile operante tra gli stessi termostati.
Ciclo di Carnot
Tralasciamo la dimostrazione del teorema e cerchiamo invece di ricostruire su un diagramma di Clapeyron P-V il ciclo di Carnot.
Teniamo presente questa considerazione: il ciclo deve essere reversibile, perciò non possiamo trasferire calore a due temperature diverse, il che equivale a dire che la macchina deve assorbire/cedere calore isotermicamente.
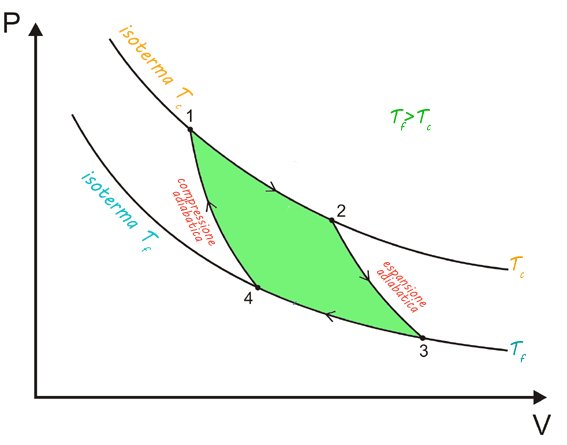
Ciclo di Carnot di un gas
Il lavoro totale compiuto dal sistema ad ogni ciclo è:
dato che gli stati 1 e 2 hanno la stessa temperatura 3 e 4 e l'energia interna dipende soltanto dalla
Il ciclo di Carnot è quindi composto da due isoterme e da due adiabatiche. Il lavoro fornito al sistema è quindi pari
Il lavoro compiuto dal gas:
che non è l'altro che l'area racchiusa (in verde sul diagramma).
Il lavoro è positivo se il ciclo è percorso in senso orario (significa che la macchina produce lavoro a spese del calore assorbito); è negativo se il ciclo è percorso in senso antiorario (la macchina produce calore a spese del lavoro compiuto).
Durante l'espansione isoterma 1-2 si ha:
Applichiamo la legge di Poisson agli stati 1-4 e 2-3, alle due adiabatiche:
dividendo membro a membro ed elevando alla 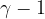 , si ottiene:
, si ottiene:
L'espressione del lavoro L allora diventa:
e sostituendo le relazioni trovate diventa:
Questo risultato significa che il rendimento del ciclo di Carnot per un gas perfetto dipende solo dalle temperature dei termostati, cioè dalle temperature estreme a cui si svolge il ciclo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





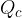 dal termostato caldo a temperatura
dal termostato caldo a temperatura 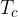 , compie lavoro L e cede il calore
, compie lavoro L e cede il calore 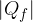 al termostato freddo a temperatura
al termostato freddo a temperatura 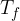 . Per completare il ciclo, il fluido di lavoro torna al suo stato iniziale. Lo scopo di ogni ciclo è produrre lavoro a spese del calore assorbito.
. Per completare il ciclo, il fluido di lavoro torna al suo stato iniziale. Lo scopo di ogni ciclo è produrre lavoro a spese del calore assorbito.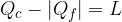
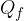 è un calore ceduto e quindi, secondo la convenzione dei segni, negativo, ma in questo caso ci interessa solo il modulo dei calori assorbiti e ceduti.
è un calore ceduto e quindi, secondo la convenzione dei segni, negativo, ma in questo caso ci interessa solo il modulo dei calori assorbiti e ceduti.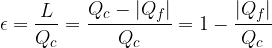

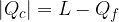
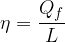

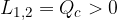
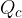 è il calore assorbito dal sistema che viene trasformato in lavoro.
è il calore assorbito dal sistema che viene trasformato in lavoro.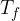 del termostato freddo nel punto 3.
del termostato freddo nel punto 3.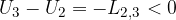
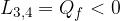
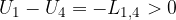
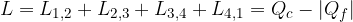

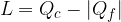
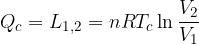
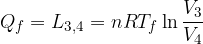
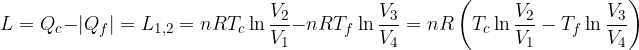

 , si ottiene:
, si ottiene: