Retta
Una retta è una linea illimitata e con una sola dimensione. Indichiamo le rette con le lettere minuscole dell'alfabeto (p, r, s, t,...):
Posizione reciproca di punti e rette
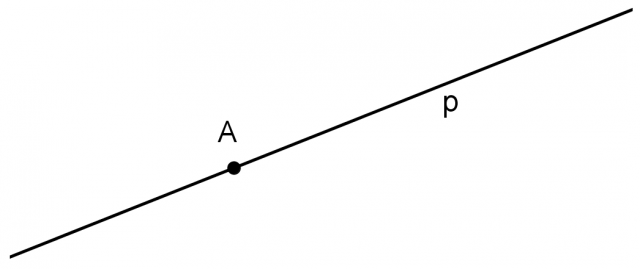
Punto appartenente ad una retta
La retta, come ogni figura del piano, è un insieme di punti. Di ogni punto del piano possiamo quindi dire se appartiene oppure no ad una retta data:
La relazione matematica che indica l'appartenenza di un punto A ad una retta p è
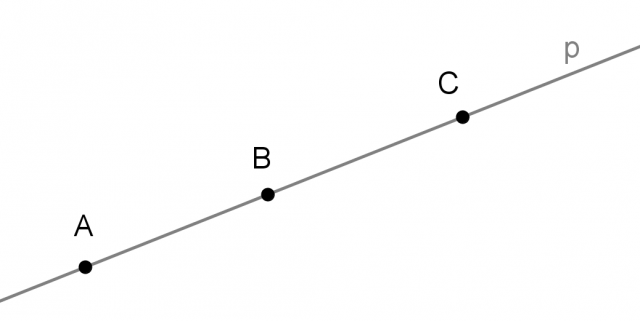
Punti distinti che appartengono alla stessa retta, si dicono allineati:
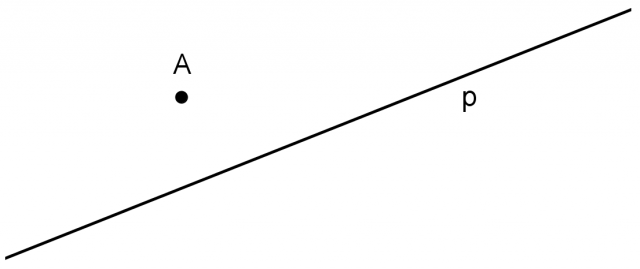
Punto esterno ad una retta
Un punto che non appartiene ad una retta si dice esterno alla retta.
La relazione matematica per indicare che il punto A non appartiene alla retta p è
Posizione reciproca delle rette nel piano
Rette parallele
Due rette appartenenti allo stesso piano si dicono parallele quando non hanno punti in comune oppure quando hanno tutti gli infiniti punti in comune.
La relazione matematica per indicare che due rette p e q sono parallele è
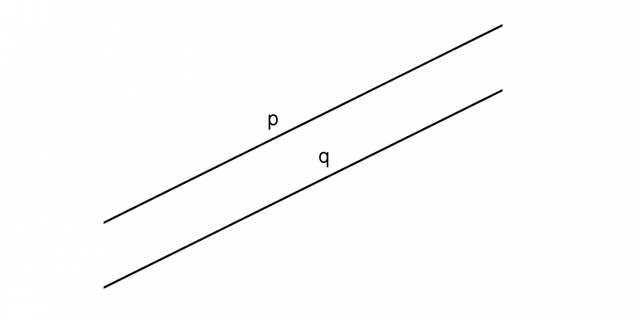
Un caso particolare di rette parallele sono le rette coincidenti. Tali rette hanno tutti gli infiniti punti in comune.
La relazione matematica per indicare che due rette p e q sono coincidenti è
Rette secanti
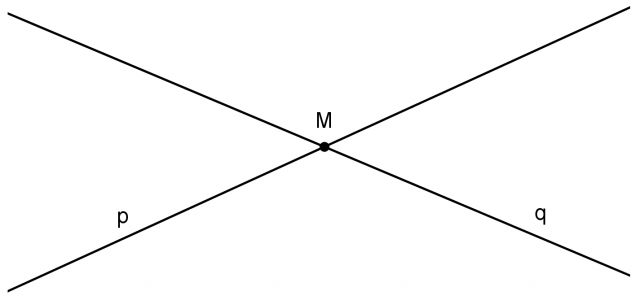
Se due rette dello stesso piano non sono nè parallele nè coincidenti, allora hanno esattamente un punto in comune. Tale punto si dice intersezione delle due rette.
La relazione matematica per indicare che le rette p e q si intersecano nel punto M è
Si dice allora che M è il punto di intersezione delle rette p e q.
Due rette che si intersecano in un punto si dicono secanti.
Rette perpendicolari
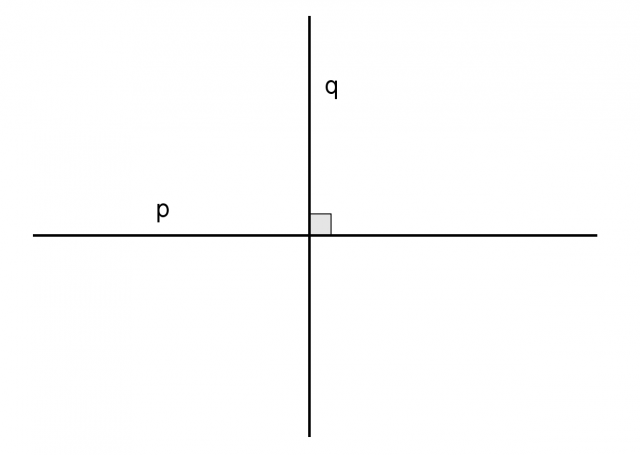
Due rette secanti si dicono perpendicolari se dividono il piano in quattro parti uguali.
Il simbolismo matematico per indicare che due rette p e qu sono perpendicolari è
Approfondimenti sulle rette perpendicolari si trovano nel capitolo Angoli nel piano.
Semirette
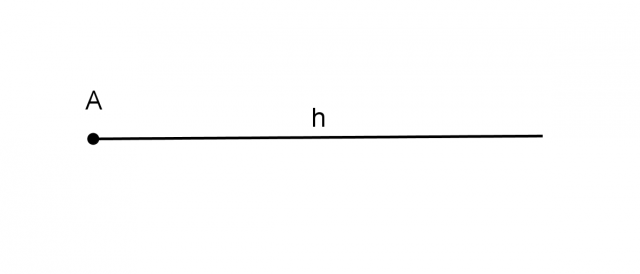
Chiamiamo semiretta una porzione continua di retta illimitata da un solo lato, e limitata da un singolo punto dall'altro lato. Tale punto si dice origine della semiretta. Indichiamo le semirette con le lettere minuscole dell'alfabeto (h, k, l,...):
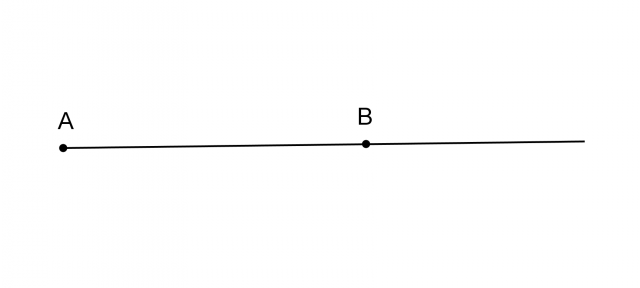
Una semiretta si può sempre indicare anche con una coppia di punti (AB, CD, EF,...), di cui il primo indica l'origine della semiretta e il secondo indica un qualunque punto appartenente alla semiretta e diverso dall'origine:
Segmenti
Un segmento è una porzione continua di retta limitata dalle due parti da due punti che si dicono estremi del segomento. Indichiamo i segmenti con i nomi dei due estremi (AB, CD, EF,...):
Distanza tra due punti
Chiamiamo distanza tra due punti la lunghezza della linea più breve che congiunge i due punti.
La linea più breve tra due punti è il segmento che li unisce. La distanza tra due punti è la lunghezza del segmento che unisce i due punti.
La distanza tra i punti A e B si indica con il seguente simbolismo matematico: 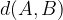 .
.
Asse di un segmento
L' asse di un segmento è una retta tale che tutti i suoi punti hanno la stessa distanza dai due estremi del segmento.
L' asse di un segmento AB interseca il segmento in un punto M che ha la stessa distanza dagli estremi A e B. Tale punto si dice punto medio del segmento.
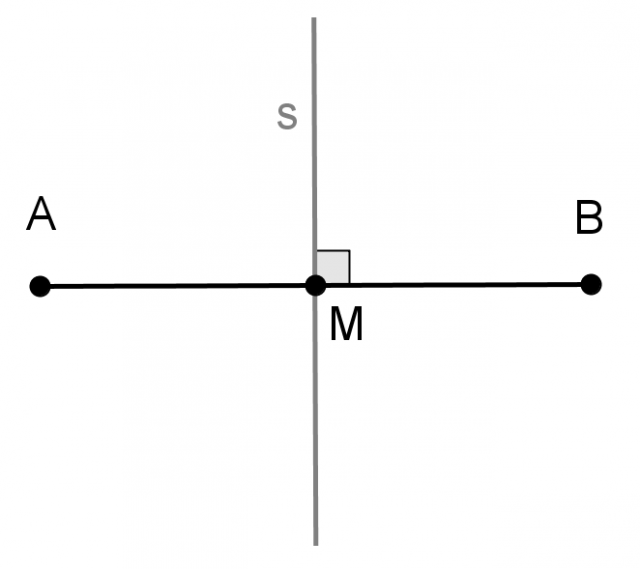
L'asse di un segmento è la retta perpendicolare passante per il punto medio




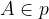
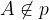
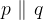
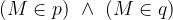
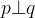

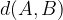 .
.



