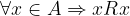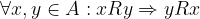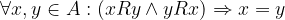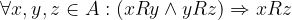Una relazione tra gli elementi di due insiemi è qualcosa in grado di collegarli, di metterli appunto in relazione, in modo ordinato e univoco.
Definizione di relazione
Dati due insieme A e B, entrambi non vuoti, si definisce relazione R un qualsiasi procedimento che associa ad alcuni elementi dell'insieme A uno o più elementi di B. Illustriamo il concetto di relazione con i seguenti esempi:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La Relazione R E' padrone di stabilisce un legame tra i cittadini italiani e i cani se i primi sono padroni dei secondi.
Relazione binaria
Dati due insiemi A e B, entrambi non vuoti, si dice che tra gli elementi di tali insieme esiste una relazione binaria R quando, presi due elementi x 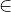 A e y
A e y 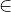 B, è valida una delle seguenti asserzioni:
B, è valida una delle seguenti asserzioni:
La coppia ordinata (x,y) soddisfa la relazione R.
La coppia ordinata (x,y) non soddisfa la relazione R.
Fissiamo il concetto con due esempi:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Vediamo un esempio di un enunciato che non è una relazione.
A: insieme dei libri di fantascienza
B: insieme dei libri di horror
L'associazione R il libro di fantascienza a è più interessante del film horror b non è una relazione in quanto può risultare vera o falsa a seconda a seconda degli interessi delle persone.
Relazione binaria su un insieme
Una relazione binaria R può essere rappresentata usando il linguaggio degli insiemi, e in particolar modo, la loro rappresentazione con i diagrammi di Eulero-Venn. Gli insiemi A e B vengono messi in relazione collegando con delle frecce gli elementi a 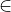 A e b
A e b 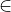 B che soddisfano la relazione R.
B che soddisfano la relazione R.
Illustriamo tale rappresentazione usando la relazione scritta prima:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
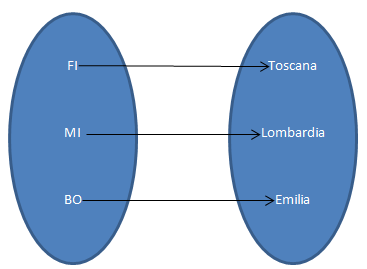
Rappresentazione della relazione E' capoluogo di
Relazione riflessiva
Una relazione R su un insieme A è riflessiva se è vera per ogni coppia (x,x).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La Relazione R riflessiva formalmente è equivalente a :
Relazione simmetrica
Una relazione R su un insieme A è simmetrica quando, se è vera per ogni coppia (x,y), allora è vera anche per la coppia (y,x).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La Relazione R simmetrica formalmente è equivalente a :
Relazione antisimmetrica
Una relazione R su un insieme A è antisimmetrica quando, se è vera per la coppia (x,y) e (y,x), deve essere vero che x=y.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La Relazione R antisimmetrica formalmente è equivalente a :
Relazione transitiva
Una relazione R su un insieme A è transitiva quando, se è vera per la coppia (x,y) e (y, z), allora è vera per la coppia (x,z).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La Relazione R transitiva formalmente è equivalente a :
Relazione di equivalenza
Una relazione R su un insieme A è di equivalenza di se risulta essere contemporaneamente:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Relazione d'ordine
Una relazione R su un insieme A è una relazione di ordine se risulta essere:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





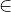 A e y
A e y 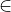 A e b
A e b