Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





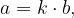
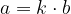 può essere scritta in modo più familiare nella seguente forma:
può essere scritta in modo più familiare nella seguente forma: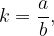
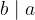
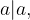
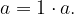
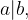 e
e 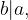 allora
allora 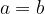
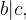 allora
allora 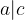 .
.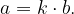
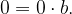
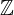
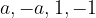
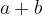
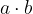
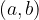 , con
, con 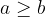 , vale il teorema della divisione euclidea.
, vale il teorema della divisione euclidea.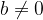 , può essere scritto come:
, può essere scritto come: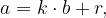
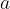 è il dividendo
è il dividendo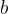 è il divisore
è il divisore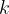 e il quoziente o rapporto
e il quoziente o rapporto è il resto, con
è il resto, con 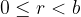 .
.


