Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





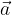 e
e 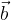 sono:
sono: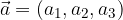
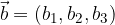
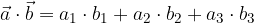
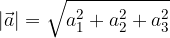
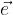 , associato ad un qualsiasi vettore
, associato ad un qualsiasi vettore