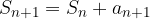Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





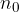 in poi e che quindi la versione che abbiamo esposto prima del principio di induzione ne è un caso particolare (
in poi e che quindi la versione che abbiamo esposto prima del principio di induzione ne è un caso particolare (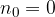 ).
).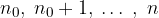 implica che A sia vera per n + 1.
implica che A sia vera per n + 1.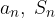 , è possibile verificare se la seconda è la successione delle somme parziali della prima - chiamata anche ridotta n-esima - (il termine generale della seconda successione è la somma dei primi n termini della prima, ovvero
, è possibile verificare se la seconda è la successione delle somme parziali della prima - chiamata anche ridotta n-esima - (il termine generale della seconda successione è la somma dei primi n termini della prima, ovvero 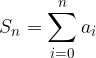 ) applicando il principio di induzione.
) applicando il principio di induzione.