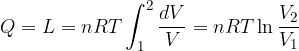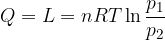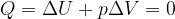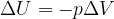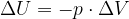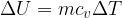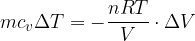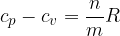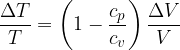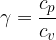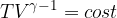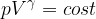Energia Interna
In meccanica la capacità di un corpo di compiere lavoro si esprime dicendo che esso possiede una certa quantità di energia E.
Anche in termodinamica un sistema possiede energia. Tale energia è chiamata energia interna U.
L'energia interna dipende dallo stato del sistema e non dalle trasformazioni (a o b o altre) compiute per raggiungere quello stato, proprio come l'energia potenziale in meccanica (che infatti dipende dalla differenza di quota del corpo e non del percorso che ha seguito).
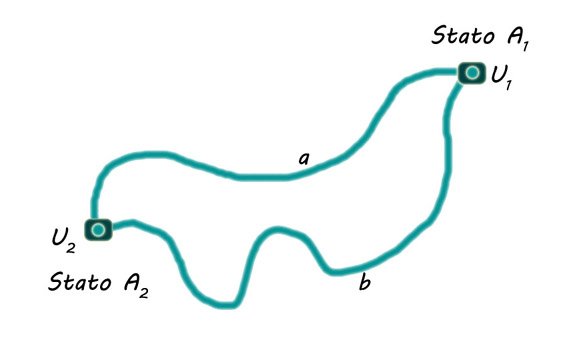
Passaggi dallo stato 1 allo stato 2
Se un sistema non isolato passa da uno stato 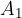 a uno stato
a uno stato 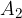 , la variazione di energia interna del sistema è:
, la variazione di energia interna del sistema è:
Come abbiamo detto, il passaggio dallo stato 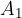 allo stato
allo stato 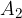 può avvenire tramite infiniti percorsi, ma il valore della variazione di energia interna è indipendente dal percorso perciò l'energia interna è una funzione di stato.
può avvenire tramite infiniti percorsi, ma il valore della variazione di energia interna è indipendente dal percorso perciò l'energia interna è una funzione di stato.
Nel caso particolare di un gas ideale l'energia interna è data dall'energia cinetica totale delle sue molecole:
Dalla formula notiamo che l'energia interna di un gas è tanto maggiore quanto maggiore è la sua temperatura.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Primo Principio della termodinamica
Secondo il Primo Principio della termodinamica l'energia può essere convertita da una forma in un'altra, ma non può essere né creata né distrutta.
Quindi, perché l'energia interna di un sistema subisca delle variazioni, ci deve essere uno scambio con l'esterno.
Gli scambi di energia con l'esterno avvengono tramite trasferimento di calore o lavoro. Infatti:
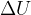 è la variazione di energia interna subita dal sistema durante la trasformazione
è la variazione di energia interna subita dal sistema durante la trasformazione
Q è la quantità di calore scambiata con l'ambiente
L è il lavoro nella trasformazione
Precisiamo però che mentre la variazione di energia interna non dipende dal percorso, i valori di Q e L presi singolarmente cambiamo da percorso a percorso. Solo la loro differenza 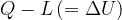 rimane uguale.
rimane uguale.
Nel caso di un gas sottoposto a una trasformazione isobara (pressione costante), il lavoro si esprime:
Primo principio della termodinamica
La variazione di energia interna di un sistema è pari alla somma algebrica degli scambi di calore e di lavoro effettuati.
Se la trasformazione è adiabatica (cioè non c'è scambio di calore con l'esterno), allora l'espressione diventa:
Se un sistema è isolato sia termicamente (Q = 0), sia meccanicamente (L = 0), la sua energia interna rimane costante.
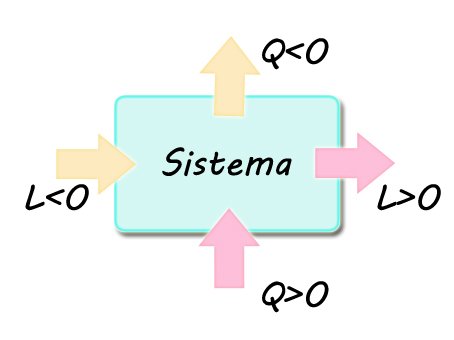
Osserviamo la convenzione dei segni degli scambi energetici:
Il calore Q è considerato positivo se acquistato dal sistema, negativo se ceduto all'ambiente.
Il lavoro L è considerato positivo se fatto dal sistema, negativo se fatto dall'ambiente.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Calore specifico e capacità termica
Il calore specifico di una sostanza è la quantità di calore necessaria per innalzare la temperatura di una unità di massa di 1 ºC (o equivalentemente di 1 K) e si misura in [J/kg K] o in [cal/g °C].
E' una proprietà intensiva caratteristica di ogni sostanza.
Ad esempio, se un grammo di rame subisse una variazione di temperatura di un grado, misureremmo una quantità di calore scambiata pari a 0,385 J/g°C. Questo valore non è altro che il calore specifico del rame.
Confrontando tale valore con quelli di altri materiali notiamo che il calore specifico del rame ha un valore piuttosto basso, ciò significa che basta poca energia per ottenere un grande aumento di temperatura.
Il calore specifico dell'acqua invece è molto alto; infatti c'è bisogno di molta energia per ottenere piccoli incrementi di temperatura.
Si definisce capacità termica di un corpo il prodotto tra il calore specifico c e alla massa m del corpo:
Possiamo definire queste due grandezze in altri termini:
La capacità termica di un corpo misura quanta energia è necessaria per aumentare di 1K (o di 1°C) la temperatura di un corpo:
Il calore specifico di una sostanza è uguale alla sua capacità termica divisa per la sua massa, esprime la quantità di energia necessaria per variare di un K la temperatura di un kg di una determinata sostanza.
Unendo insieme le due relazioni è possibile ricavare la quantità di calore Q trasmessa ad un corpo:
La precedente espressione indica che fornendo del calore Q a una massa m, si ha una variazione di temperatura direttamente proporzionale al calore fornito e dipendente dal calore specifico c (caratteristico di ciascuna sostanza).
Calore specifico molare
Se il calore specifico viene espresso per mole di sostanza e non per grammo, allora si parla di calore specifico molare.
Tale grandezza è definita, analogamente alla precedente, come la quantità di calore necessaria per aumentare di 1 ºC (o equivalentemente di 1 K) la temperatura di una mole di sostanza.
L'unità di misura è il [J/(mol K)] o [J/(mol °C)].
Il calore Q assorbito o ceduto da n moli di una sostanza per variare la sua temperatura è:
dove 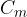 rappresenta il calore specifico molare.
rappresenta il calore specifico molare.
Per i gas distinguiamo calore specifico molare a volume costante e a pressione costante.
Per una trasformazione isocora avremo:
Calore specifico molare del gas perfetto a volume costante - trasformazione isocora
Secondo il primo principio della termodinamica la variazione di energia interna è la somma algebrica del calore e del lavoro scambiati nella trasformazione:
Ma se il volume del gas rimane costante allora non si compie lavoro e la variazione di energia interna è semplicemente pari al calore Q:
In una trasformazione a volume costante la variazione di energia interna è pari al calore scambiato nella trasformazione.
Possiamo calcolare il calore Q scambiato a volume costante utilizzando il calore specifico molare a volume costante:
E dato che in questo caso il calore è pari alla variazione di energia interna:
Semplifichiamo e otteniamo che il calore specifico a volume costante in un gas perfetto monoatomico vale:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trasformazione a pressione costante - trasformazione isobara
Nella figura è rappresentato un contenitore riempito di un gas ideale riscaldato con una quantità di calore Q. La sommità del contenitore è chiusa da un pistone che può scorrere liberamente lasciando che il gas si possa espandere mantenendo costante la pressione.
Il gas quindi si espande e compie del lavoro, perciò una parte del calore Q fornito incrementa l’energia interna, mentre una parte viene spesa per eseguire il lavoro per espandere il gas.
Dal momento che solo una parte del calore viene usata per incrementare la temperatura (cioè l’energia interna), allora per avere lo stesso incremento di temperatura che si avrebbe a volume costante, occorre fornire più calore. Questo significa che il calore specifico a pressione costante è maggiore di quello a volume costante, cioè che per innalzare di un grado la temperatura di una mole di gas perfetto a pressione costante occorre più calore che per innalzare di un grado la temperatura della stesso gas a volume costante:
Applichiamo il Primo principio:
il lavoro a pressione costante vale:
e la variazione di energia interna:
Applicando la definizione di calore specifico molare:
eguagliando le due espressioni:
si ottiene il calore specifico molare a pressione costante di un gas perfetto:
Nel modello dei gas perfetti il calore specifico molare vale:
Relazione tra calore specifico a pressione costante e a volume costante
Abbiamo visto che per i gas il calore specifico molare a pressione costante è maggiore di quello a volume costante e il motivo risiede nel fatto che parte del calore nella trasformazione isobara viene impiegato come lavoro per espandere il gas, in altri termini quindi c'è bisogno di più calore per ottenere la stessa variazione di temperatura.
Se riusciamo a quantificare quanto valga questa differenza troveremo una relazione tra i due calori specifici.
Il calore che dobbiamo fornire a una mole di gas a pressione esterna costante per per aumentare di 1 K la sua temperatura è:
La variazione di volume è data da:
In questo caso la variazione di temperatura è di un grado, perciò possiamo semplificare:
Sostituiamo nell'equazione dei calori specifici:
Il secondo termine è pari alla costante dei gas R, perciò:
Questa relazione tra i calori specifici è nota come relazione di Mayer.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Altri tipi di trasformazione
Le trasformazioni che può subire un sistema termodinamico sono infinite e differiscono l'una dall'altra per come variano le coordinate termodinamiche che lo definiscono.
Per i fluidi (liquidi e gas) ce ne sono alcune molto importanti, oltre alle trasformazioni isocore e isobare.
Trasformazione isoterma
Significa che la trasformazione avviene a temperatura costante. Se la temperatura non subisce variazioni allora anche l'energia interna non subisce variazioni:
Osserviamo cosa succede applicando il Primo Principio:
Se 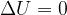 allora:
allora:
Cioè il calore ricevuto è pari al lavoro.
Per un gas perfetto la curva che descrive la trasformazione isoterma in un diagramma di Clapeyron è un ramo di iperbole che ha per asintoti gli assi coordinati.
Allora il lavoro sarà dato dall'area sottesa alla curva tra i valori di volume considerati.
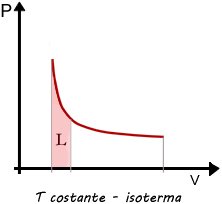
Lavoro in una trasformazione isoterma
l'espressione del lavoro diventa:
Si tratta quindi di integrare tra i valori di volume 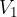 e
e 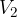 :
:
Per la Legge di Boyle si ha anche:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Trasformazione adiabatica
Questo tipo di trasformazione è caratterizzata dal fatto che non scambia calore con l'ambiente:
Equazione di Poisson
Per le trasformazioni adiabatiche reversibile vale:
Sostituendo all'energia interna l'espressione relativa a una trasformazione isocora:
e al secondo membro ciò che si ottiene dall'equazione di stato:
Che vale per qualsiasi massa di gas.
Sfrttando la relazione dell'equazione di stato si ottiene anche:
che viene ricordata come Equazione di Poisson.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





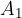 a uno stato
a uno stato 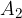 , la variazione di energia interna del sistema è:
, la variazione di energia interna del sistema è: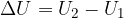
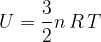
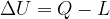
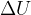 è la variazione di energia interna subita dal sistema durante la trasformazione
è la variazione di energia interna subita dal sistema durante la trasformazione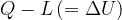 rimane uguale.
rimane uguale.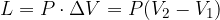
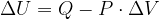
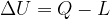
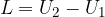
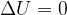
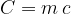
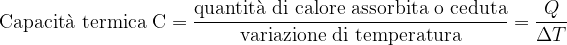
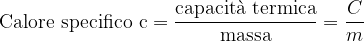
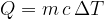
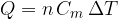
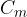 rappresenta il calore specifico molare.
rappresenta il calore specifico molare.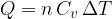
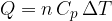
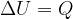
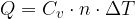
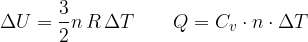
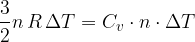
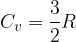

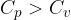
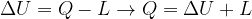
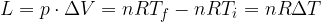
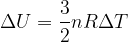
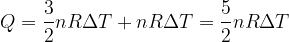
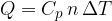
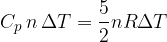
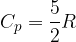
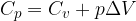
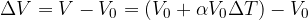
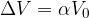
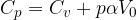
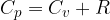
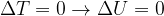
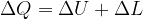
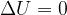 allora:
allora: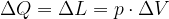

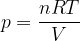
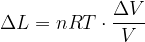
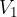 e
e 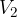 :
: