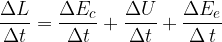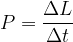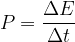Quando viene compiuto un lavoro è importante conoscerne la quantità prodotta e in quanto tempo tale lavoro è stato fatto. In altre parole, oltre alla quantità di lavoro è utile sapere anche con quale rapidità è stato effettuato.
Definiamo quindi la potenza meccanica come il lavoro per unità di tempo:
L'unità di misura della potenza è il Watt:
un Watt è un Joule al secondo.
Possiamo esprimere il lavoro in funzione della potenza:
di conseguenza i Joule possono essere anche espressi come:
La potenza è il lavoro per unità di tempo:
La sua unità di misura è:
Potenza e moto traslatorio
Se dividiamo entrambi i membri per 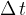 otteniamo:
otteniamo:
Ricordando che la potenza è:
e la velocità istantanea:
possiamo esprimere la potenza come il prodotto della forza per la velocità:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Possiamo esprimere la potenza come il prodotto della forza per la velocità:
Potenza e moto rotazionale
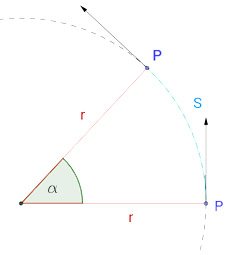
Consideriamo un corpo che ruota intorno a un asse con una certa velocità angolare 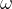 . Possiamo calcolare lo spazio che percorre come:
. Possiamo calcolare lo spazio che percorre come:
il termine 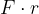 , è il momento M della forza, quindi:
, è il momento M della forza, quindi:
Possiamo allora calcolare la potenza:
sostituiamo l'espressione della velocità angolare:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La potenza nel moto rotatorio si esprime come prodotto della coppia e della velocità angolare:
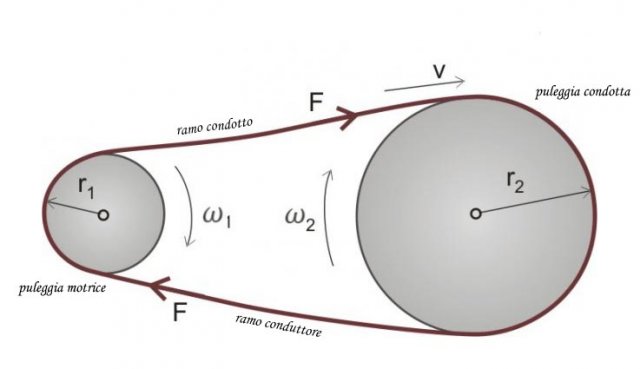
Trasmissione della potenza con organi flessibili
Gli organi flessibili sono cinghie, catene e funi che collegano due pulegge trasmettendo la potenza di una all'altra
In figura, a sinistra c'è la puleggia motrice che trascina (per attrito) la cinghia che a sua volta fa girare la seconda puleggia (quella a destra in figura). Le due pulegge quindi girano nello stesso verso ognuna con la propria velocità angolare 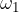 e
e 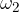 .
.
Il ramo conduttore è quello che va verso la puleggia motrice, il ramo condotto è quello che va verso la puleggia condotta.
Facciamo alcune osservazioni:
La forza F lungo la cinghia è la stessa ovunque, poiché questa è una forza interna.
Le velocità angolari delle pulegge sono inversamente proporzionali ai raggi.
La velocità della cinghia v (se non ci sono slittamenti) è pari alla velocità periferica delle pulegge. Quindi:
Su entrambe le pulegge agisce la stessa forza.
Riprendiamo l'espressione della potenza in funzione della velocità: 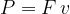 , se la forza e la velocità sono uguali su entrambe le pulegge, allora lo deve essere anche la potenza.
, se la forza e la velocità sono uguali su entrambe le pulegge, allora lo deve essere anche la potenza.
Il momento delle pulegge è direttamente proporzionale al raggio e inversamente proporzionale alla velocità angolare.
Scriviamo la formula del momento di una forza
facciamo il rapporto delle due espressioni e otteniamo:
Si consideri l'equazione:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Velocità angolare e raggio
Coppia e velocità angolare
il pedice 1 indica la puleggia motrice, il pedice 2 la puleggia condotta
Potenza ed energia
Nel capitolo sull'energia elastica è stata definita la legge di conservazione dell'energia:
Se dividiamo entrambi i membri per 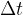 otteniamo:
otteniamo:
Notiamo che il primo membro non è altro che la potenza:
Mentre la somma al numeratore del secondo membro è l'energia totale E, perciò:
La potenza quindi dà una misura di quanto velocemente varia l'energia totale di un corpo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La potenza dà una misura di quanto velocemente varia l'energia totale di un corpo




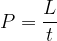
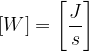
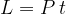
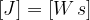
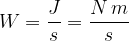
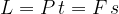
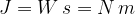
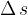 in un intervallo di tempo
in un intervallo di tempo 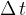 compie un lavoro
compie un lavoro 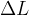 :
: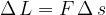
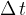 otteniamo:
otteniamo: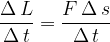
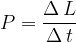
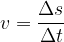
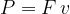
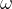 . Possiamo calcolare lo spazio che percorre come:
. Possiamo calcolare lo spazio che percorre come: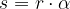
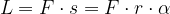
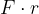 , è il momento M della forza, quindi:
, è il momento M della forza, quindi: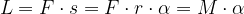
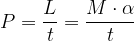
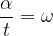
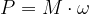
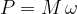
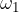 e
e 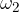 .
.
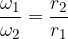
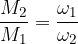
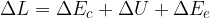
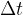 otteniamo:
otteniamo: