Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





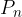 è dato dal prodotto di tutti i numeri consecutivi da 1 a n:
è dato dal prodotto di tutti i numeri consecutivi da 1 a n: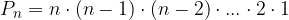
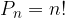
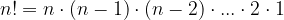
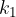 volte, un secondo elemento si ripete
volte, un secondo elemento si ripete 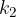 volte, ... e l'r-esimo elemento si ripete
volte, ... e l'r-esimo elemento si ripete 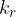 volte.
volte.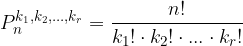
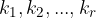 che rappresentano quante volte ogni elemento si ripete deve essere sempre uguale a n:
che rappresentano quante volte ogni elemento si ripete deve essere sempre uguale a n:



