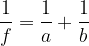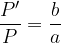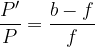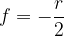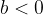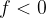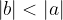L’ottica geometrica analizza la formazione delle immagini assumendo che la luce si propaghi in modo rettilineo sfruttando i fenomeni di riflessione e rifrazione, è perciò un’approssimazione dell’ottica fisica (o ondulatoria) perché vengono trascurati gli effetti della diffrazione in quanto la lunghezza d'onda della luce è più piccola delle dimensioni degli ostacoli o delle aperture che incontra.
Vediamo ora cosa succede quando le onde luminose incidono su delle superfici piane o curve. Attraverso la riflessione o la rifrazione si formano delle immagini. Gli specchi formano immagini per riflessione, le lenti invece per rifrazione.
Specchi piani
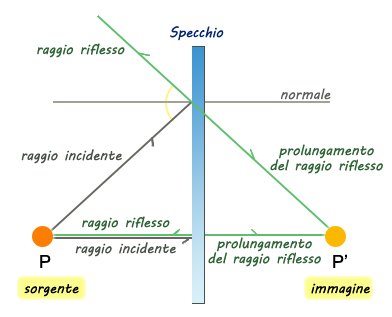
Consideriamo due raggi che partono da una sorgente P. Sappiamo dalla legge di riflessione che il raggio riflesso forma con la normale alla superficie un angolo pari all'angolo incidente.
Prolungando i raggio riflessi oltre la superficie, i prolungamenti si intersecheranno in un punto P'.
Da notare che la distanza dalla superficie dello specchio di P e di P' è uguale.
I raggi riflessi dallo specchio piano sembrano provenire dal punto P' oltre lo specchio: tale punto è l'immagine virtuale di P.
In uno specchio piano l'immagine:
dista dallo specchio quanto l’oggetto posto di fronte allo specchio
inverte la destra e la sinistra
Specchi sferici
La superficie di uno specchio sferico è una piccola parte di una superficie sferica. Se la parte riflettente della superficie è quella esterna si ha uno specchio convesso, mentre se è quella interna si ha uno specchio concavo.
Vediamo nella figura quali sono gli elementi fondamentali da conoscere per lo studio degli specchi sferici:
la normale è la perpendicolare al piano tangente alla superficie sferica nel punto di incidenza
il centro di curvatura e il raggio di curvatura sono il centro della sfera O e il suo raggio r.
l’asse ottico dello specchio è il suo asse di simmetria, cioè la retta che congiunge il centro di curvatura O con il centro dello specchio V.
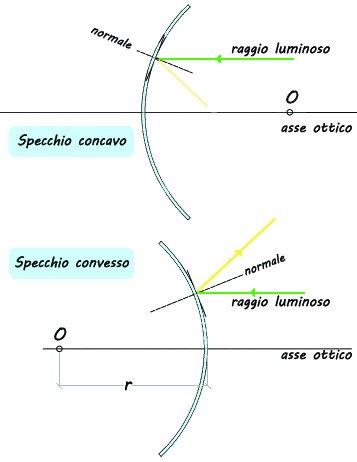
Specchi sferici convessi e concavi
La legge della riflessione per gli specchi piani è valida anche per gli specchi sferici.
Specchi sferici concavi
Nella figura vediamo uno specchio sferico concavo e una torre posizionata oltre il suo centro ottico O in modo che alcuni suoi punti si trovano sull'asse. I raggi che provengono da quei punti si riflettono sullo specchio seguendo la legge di riflessione (cioè, i raggi riflessi hanno lo stesso angolo dei raggi incidenti rispetto alla normale alla superficie) e convergono in un punto chiamato punto immagine.
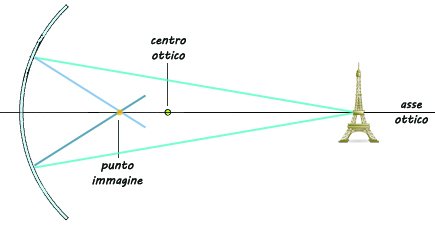
Specchio concavo: punto immagine
Se la torre (o in generale una sorgente) fosse posta all'infinito sull'asse ottico i raggi che provengono sarebbero paralleli all'asse ottico dello specchio (raggi parassiali). e convergerebbero in un punto chiamato fuoco.
Viceversa, se la sorgente è nel fuoco F, i raggi riflessi sono paralleli all'asse ottico per il Principio di reversibilità del cammino ottico.
Principio di reversibilità dei cammini ottici:
se si inverte il verso di un raggio luminoso, il raggio ripercorre il cammino originale.
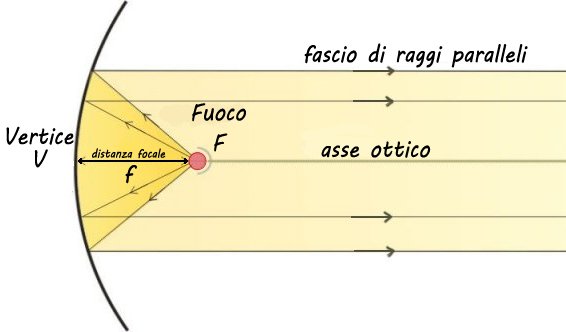
Specchio concavo: punto focale o fuoco F
Distanza focale
La distanza tra il fuoco e il centro dello specchio è chiamata distanza focale f dello specchio. Il fuoco F di uno specchio concavo si trova nel punto medio del segmento che congiunge il centro di curvatura O e il centro dello specchio V:
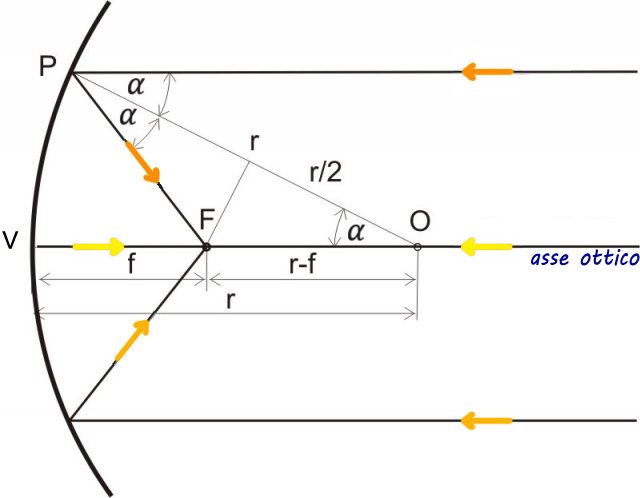
Specchio concavo: i raggi paralleli all'asse ottico si intersecano nel fuoco F
Consideriamo un raggio parallelo all'asse ottico che incide sullo specchio nel punto P, collegando il punto P con in centro O dello specchio non solo troviamo il raggio r dello specchio ma individuiamo anche la normale alla suoerficie, per la legge di riflessione l'angolo 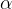 di incidenza è pari all'angolo di riflessione.
di incidenza è pari all'angolo di riflessione.
L'angolo 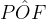 essendo alterno interno all'angolo di incidenza è pari ad
essendo alterno interno all'angolo di incidenza è pari ad 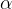 , perciò il triangolo PFO è isoscele di base r. L'altezza del triangolo interseca la linea di base a metà, cioè a r/2. Ora possiamo calcolare la distanza focale osservando dalla figura che l'altezza è pari al coseno della distanza OF:
, perciò il triangolo PFO è isoscele di base r. L'altezza del triangolo interseca la linea di base a metà, cioè a r/2. Ora possiamo calcolare la distanza focale osservando dalla figura che l'altezza è pari al coseno della distanza OF:
Vediamo quindi che la distanza focale dipende dal coseno dell'angolo di incidenza, ma per raggi molto vicini all'asse ottico il coseno di tale angolo è circa pari all'unità per cui ne deriva che in questo specifico caso la distanza focale è pari alla metà del raggio.
I raggi molto distanti dall'asse però non convergono precisamente nel fuoco di uno specchio sferico e le immagini che si ottengono non sono nitide; questo fenomeno si chiama aberrazione sferica e può essere eliminata utilizzando specchi parabolici. Il motivo è semplice, la parabola per definizione ha un unico fuoco e tutti i raggi paralleli all'asse ottico, dopo essere stati riflessi, convergono in un unico punto immagine, indipendentemente dalla loro distanza dall'asse ottico. Le immagini che si ottengono sono nitide e precise, per questo gli specchi parabolici vengono utilizzati nei telescopi.
Costruzione dell'immagine di uno specchio concavo
Per costruire un'immagine, determinandone sia la posizione che le dimensioni, prodotta da uno specchio possiamo utilizzare un metodo grafico, chiamato diagramma dei raggi, che sfrutta la legge di riflessione e i concetti di curvatura e fuoco di uno specchio sferico.
Consideriamo tre raggi particolari, rappresentati nella figura e denominati con i pedici 1, 2, 3:
Raggio 1 - raggio parallelo: raggio incidente parallelo all'asse ottico dello specchio, il suo raggio riflesso passa per il fuoco F
Raggio 2 - raggio focale: raggio incidente passante per il fuoco F e poi riflesso come raggio parallelo all'asse ottico.
Raggio 3 - raggio del centro: raggio incidente passante per il centro di curvatura O, ha la direzione di un raggio perpendicolare alla superficie dello specchio perciò il raggio riflesso segue lo stesso percorso di quello incidente.
Di questi tre raggi due servono per il disegno, uno per il controllo.
Disegniamo il Diagramma dei raggi:
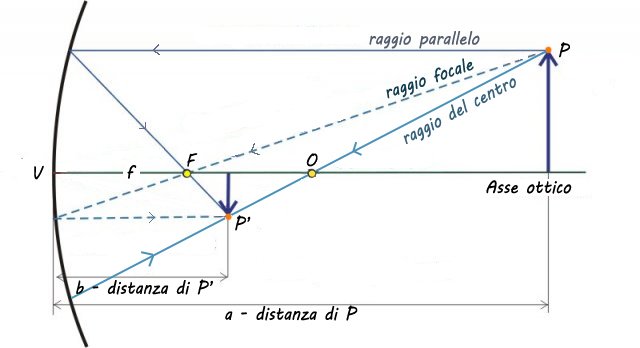
Oggetto posizionato oltre il centro ottico riflesso in uno specchio concavo
Disegnando i raggi in un unico disegno vediamo che essi si intersecano in un punto che è proprio l’immagine della punta della freccia.
Per trovare le immagini di altri punti della freccia si procede in modo analogo: si disegnano cioè i tre raggi relativi al punto da ottenere. L’immagine completa rappresenta la freccia è reale, capovolta e rimpicciolita rispetto all'oggetto.
Se nella figura si scambia la posizione dell’oggetto P con quella dell’immagine P' si ottiene la situazione rappresentata in figura:
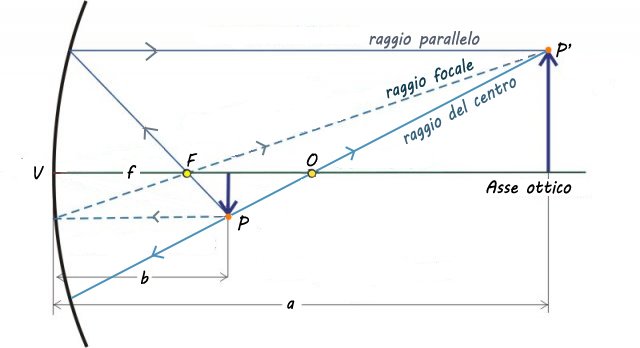
Oggetto posizionato tra il centro ottico e il fuoco riflesso in uno specchio concavo
Quindi se l'oggetto è posto tra il centro di curvatura O e il fuoco F si ottiene un’immagine reale (perché i raggi luminosi passano per il punto immagine), ingrandita e capovolta.
Se invece l'oggetto si trova tra il fuoco e il centro dello specchio i prolungamenti dei tre raggi riflessi si intersecano oltre lo specchio e l'immagine che si forma è virtuale, diritta e ingrandita rispetto all'oggetto.
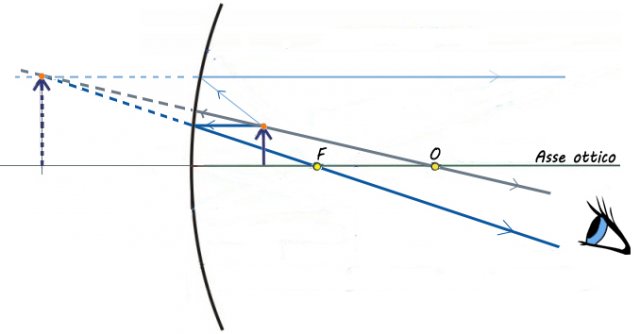
Oggetto posizionato tra il centro dello specchio e il fuoco riflesso in uno specchio concavo
L'equazione dei punti coniugati
I diagrammi dei raggi servono per determinare graficamente la posizione e la dimensione dell’immagine formata da uno specchio, ma per descrivere le caratteristiche dell'immagine abbiamo bisogno di ricavare una relazione matematica che leghi ogni punto dell'oggetto P al corrispondente punto P' (punto coniugato) dell'immagine.
Tale relazione è chiamata equazione dei punti coniugati:
dove f è la distanza focale, a è la distanza del'oggetto dallo specchio e b la distanza dell'immagine dallo specchio.
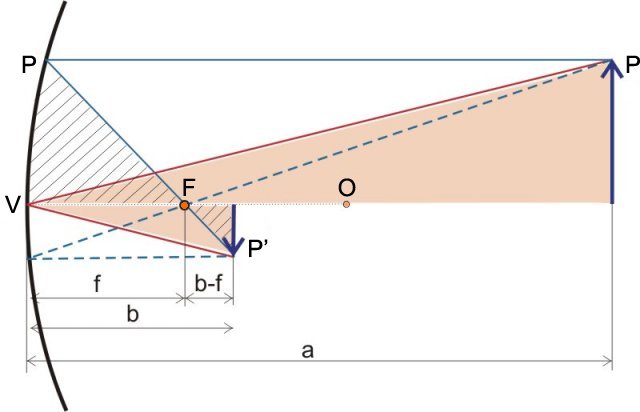
L'equazione dei punti coniugati: i raggi formano triangoli simili.
Osserviamo che i due triangoli campiti di rosa sono simili, e perciò l'altezza individuata da P e da P' sta in un certo rapporto in cui stanno le loro distanze a e b dal vertice:
dove P è l'altezza dell'oggetto, e P' l'altezza dell'immagine.
Consideriamo ora le aree tratteggiate in grigio. Anche questi due triangoli possono essere considerati simili. In realtà è un'approssimazione ma sarà tanto più vicina alla realtà quanto più il raggio incidente è parallelo e vicino all'asse ottico dello specchio.
La dimensione dell'immagine e dell'oggetto sono nella stessa proporzione della loro distanza dal fuoco F dello specchio:
Possiamo eguagliare le due equazioni:
Le equazioni dello specchio sono:
P è l'altezza dell'oggetto, e P' l'altezza dell'immagine
f è la distanza focale, a è la distanza del'oggetto dallo specchio e b la distanza dell'immagine dallo specchio
Il rapporto P'/P è chiamato ingrandimento:
P'/P >0 l'immagine è capovolta
P'/P <0 l'immagine è diritta
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
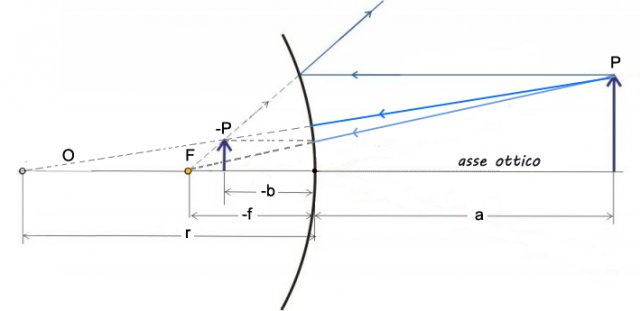
Specchio sferico convesso
Uno specchio convesso forma sempre immagini virtuali qualsiasi sia la posizione dell'oggetto. Un'altra caratteristica di questi specchi è che le immagini virtuali risultano rimpicciolite determinando un campo visivo maggiore; infatti questo tipo di specchio viene usato negli specchietti retrovisori delle automobili.
Anche per gli specchi convessi possiamo utilizzare il diagramma dei raggi, in questo caso però il fuoco e il centro di curvatura si trovano dietro lo specchio, dalla parte opposta rispetto all'oggetto.
Distanza focale
Determiniamo la relazione che lega la distanza focale (distanza tra il fuoco e il centro dello specchio) e il raggio di curvatura. Sappiamo che i raggi paralleli all'asse ottico che incidono sulla superficie dello specchio vengono riflessi in direzioni che divergono rispetto all'asse ottico, ma se consideriamo dei raggi parassiali (cioè paralleli e molto vicini all'asse ottico) vedremo che i raggi riflessi sembrano provenire dal fuoco F, dietro lo specchio.
Anche la distanza focale di uno specchio convesso è uguale alla metà del raggio di curvatura, ma per convenzione si indica col segno negativo:
Costruzione dell'immagine di uno specchio convesso
Vediamo quali raggi utilizzare per costruire il diagramma:
Raggio 1 - raggio parallelo: raggio incidente parallelo all'asse ottico dello specchio, il suo raggio riflesso passa per il fuoco F
Raggio 2 - raggio focale: il prolungamento di questo raggio passa per il fuoco e viene poi riflesso come raggio parallelo all'asse ottico
Raggio 3 - raggio del centro: raggio incidente passante per il centro di curvatura O, ha la direzione di un raggio perpendicolare alla superficie dello specchio perciò il raggio riflesso ha la stessa direzione di quello incidente ma verso opposto.
Disegniamo il Diagramma dei raggi:
Osserviamo nella figura che l'immagine che si forma è virtuale (posta dietro allo specchio), diritta e rimpicciolita rispetto all'oggetto.
Equazione dei punti coniugati
Anche in questo caso è valida l'equazione dei punti coniugati, l'unica accortezza è di considerare negativa la distanza focale.
L'immagine di uno specchio convesso è sempre virtuale, diritta e rimpicciolita, qualsiasi sia la posizione dell'oggetto davanti allo specchio.
La distanza focale e la distanza dell'immagine dallo specchio sono prese col segno negativo per convenzione:
Il valore assoluto della distanza dell'immagine dallo specchio b è sempre inferiore alla distanza dell'oggetto a:
Ne consegue che l'immagine è sempre più piccola dell'oggetto dato che:
Se l'oggetto è posto all'infinito l'immagine virtuale si forma nel fuoco dello specchio.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
f>0 per uno specchio concavo
f<0 per uno specchio convesso
a>0 se l’oggetto è davanti allo specchio (oggetto reale)
a<0 se l’oggetto è dietro lo specchio (oggetto virtuale)
b>0 se l’immagine è davanti allo specchio (immagine reale)
b<0 se l’immagine è dietro lo specchio (immagine virtuale)
P'/P >0 l'immagine è capovolta
P'/P <0 l'immagine è diritta







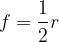

 di incidenza è pari all'angolo di riflessione.
di incidenza è pari all'angolo di riflessione. essendo alterno interno all'angolo di incidenza è pari ad
essendo alterno interno all'angolo di incidenza è pari ad