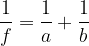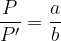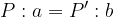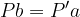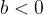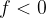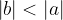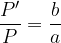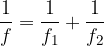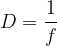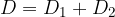Le lenti sono dispositivi ottici che sfruttano la rifrazione.
Abbiamo visto che quando la luce incide su una superficie di separazione tra un mezzo meno denso (ad esempio l'aria) a un mezzo più denso (ad esempio il vetro) la velocità della luce nel mezzo più denso diminuisce e i raggi rifratti si avvicinano alla normale alla superficie di separazione.
Le lenti che verranno studiate in questo capitolo sono lenti sferiche sottili, lenti cioè delimitate da due superfici sferiche con uno spessore molto più piccolo dei raggi delle superfici sferiche che le delimitano.
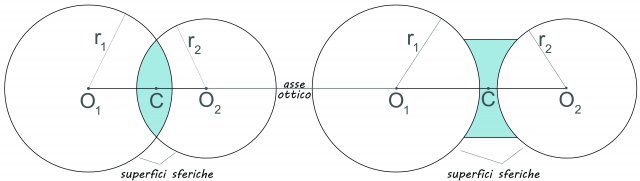
Lenti sferiche convesse e concave
Le lenti sono impiegate in molti strumenti ottici, come occhiali, macchine fotografiche e telescopi.
Vediamo in dettaglio due tipi di lenti sottili: le lenti convergenti e le lenti divergenti.
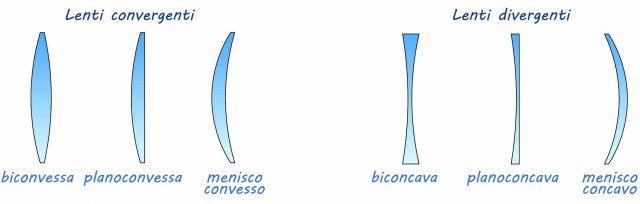
Le lenti convergenti sono più spesse al centro. Le lenti divergenti sono più sottili al centro che ai bordi.
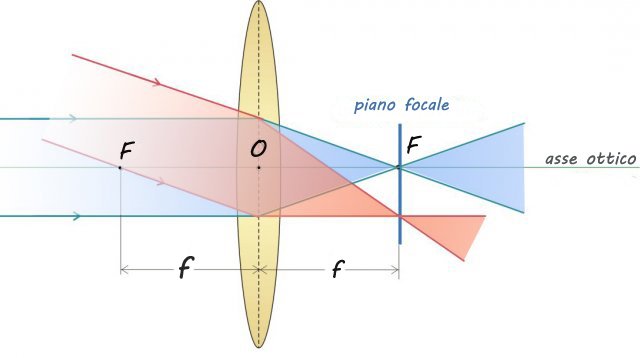
Una lente convergente devia i raggi che incidono su di essa parallelamente all'asse ottico e li fa convergere in un punto sull'asse ottico detto fuoco F.
Una lente convergente
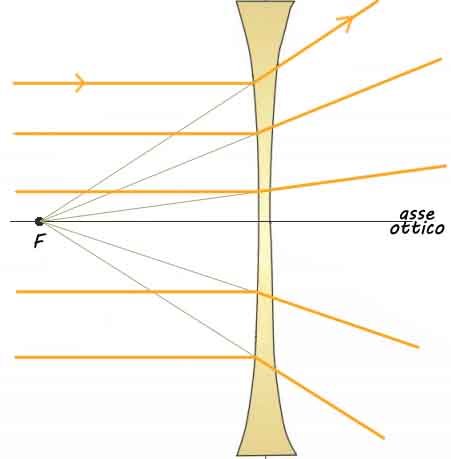
Una lente divergente devia i raggi che incidono su di essa parallelamente all'asse ottico e li fa divergere come se provenissero da un punto sull'asse ottico, detto fuoco F.
Una lente divergente
Come abbiamo fatto per gli specchi, anche per le lenti possiamo utilizzare i diagrammi dei raggi per determinare la posizione e le dimensioni di un'immagine. L'unica differenza è che nelle lenti i raggi luminosi possono incidere su entrambe le facce. Per questo dobbiamo conoscere la posizione dei due fuochi (si trovano sull'asse ottico a una distanza dalla lente pari alla distanza focale).
L'oggetto (per esempio una freccia) è posto sinistra della lente.
Raggio 1: raggio incidente è parallelo all'asse ottico. Il raggio attraversa la lente e converge nel fuoco a destra
Raggio 2: raggio incidente passante per il fuoco a sinistra della lente e rifratto in direzione parallela all'asse ottico
Raggio 3: raggio incidente diretto verso il centro della lente sottile. Il raggio attraversa la lente senza essere deviato
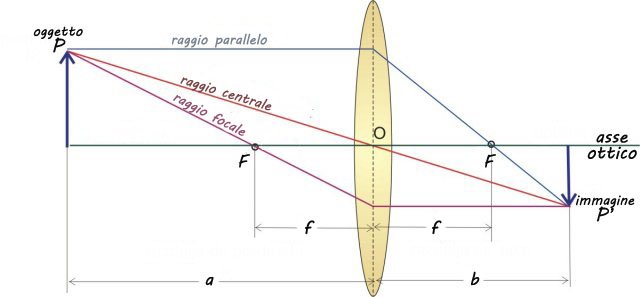
Diagramma dei raggi di una lente convergente
Il diagramma dei raggi mostra che l’immagine dell’oggetto è reale, capovolta e rimpicciolita rispetto all'oggetto.
L'oggetto (per esempio una freccia) è posto sinistra della lente.
Raggio 1: raggio incidente è parallelo all'asse ottico. Dopo aver attraversato la lente il raggio rifratto sembra provenire dal fuoco a sinistra della lente
Raggio 2: raggio incidente diretto verso il fuoco a destra della lente e rifratto parallelamente all'asse ottico
Raggio 3: raggio incidente diretto verso il centro della lente sottile. Il raggio attraversa la lente senza essere deviato
Nel caso di una lente concava, i raggi dopo aver attraversato la lente divergono, infatti si intersecano solo i prolungamenti dei raggi reali.
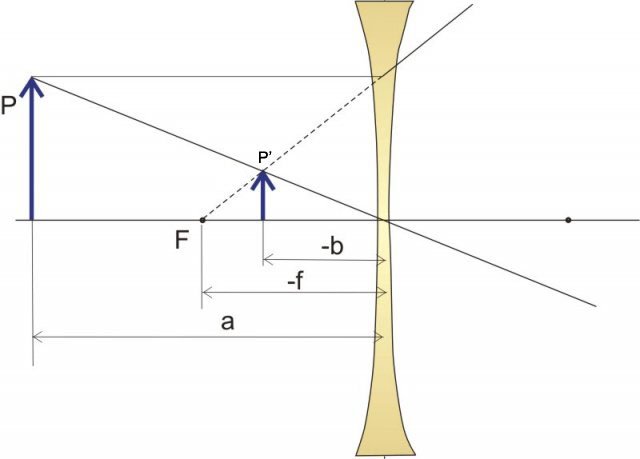
Diagramma dei raggi di una lente divergente
Il diagramma dei raggi indica che si forma un'immagine virtuale a sinistra della lente. In effetti, indipendentemente dalla posizione dell’oggetto, una lente divergente forma sempre un’immagine virtuale, diritta e rimpicciolita rispetto all'oggetto.
Vediamo ora alcuni concetti e termini utilizzati per tutte le lenti (non solo convesse).
Concetti di base nel trattamento di lenti:
Il centro della lente è il punto al centro della lente e indicato con O
La distanza tra il fuoco e il centro di una lente è chiamata distanza focale f della lente
L'asse ottico è una linea retta passante per il centro della lente ed è perpendicolare alla superficie della lente
La lente ha due punti focali: uno a sinistra e una a destra del centro della lente
Per determinare con precisione le caratteristiche dell’immagine di un oggetto formata da una lente sottile si possono usare le due seguenti equazioni:
Equazione delle lenti sottili:
Equazione dell’ingrandimento lineare:
Vediamo ora come possiamo ricavare l'equazione delle lenti sottili:
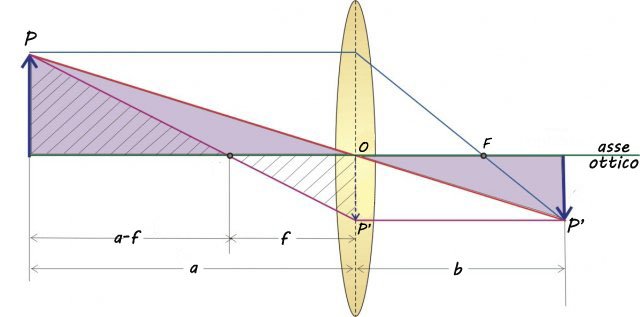
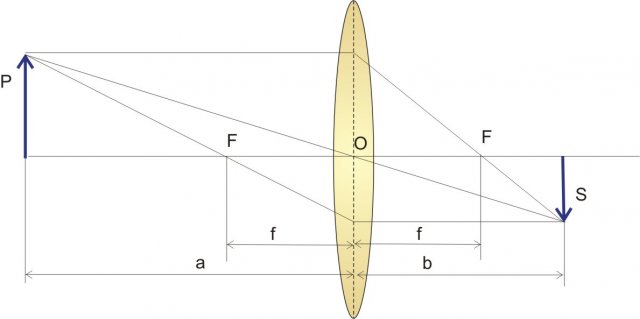
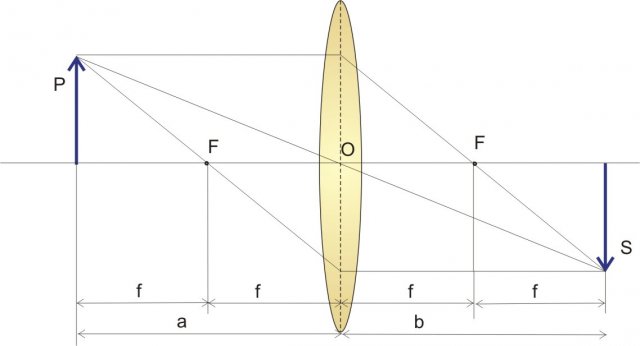
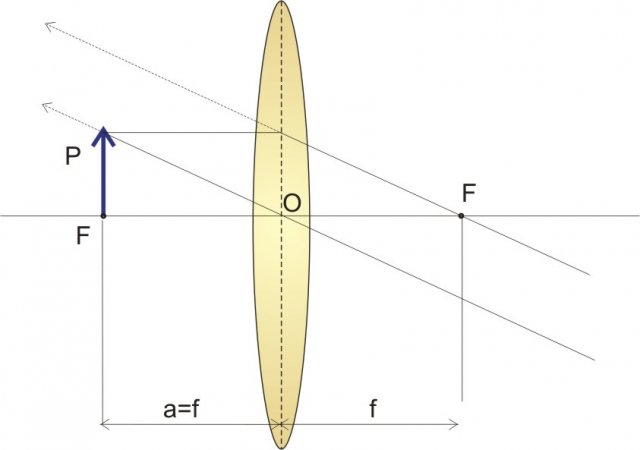
Equazione delle lenti sottili: i raggi formano triangoli simili.
Osserviamo l'area campita in viola: i due triangoli sono simili perché sono due triangoli rettangoli con gli angoli al vertice congruenti. L'altezza dei due triangoli non è altro che la dimensione dell'oggetto e la base la distanza dell'oggetto e dell'immagine dalla lente, perciò:
cioè:
da cui:
dove P è la dimensione dell'oggetto, P' è la dimensione dell'immagine.
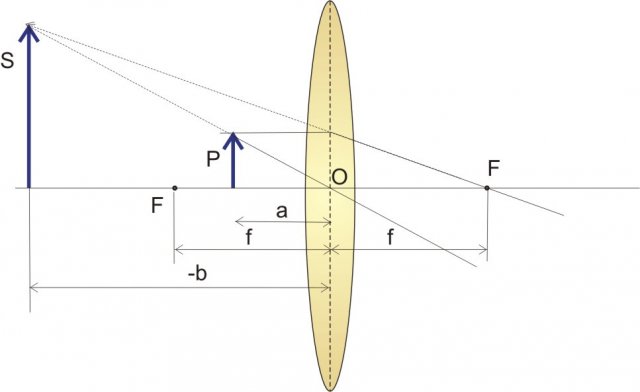
Osserviamo ora l'area tratteggiata: i due triangoli sono simili per i motivi già ricordati, perciò:
Le equazioni delle lenti sono:
dove:
P è la dimensione dell'oggetto
a è la sua distanza dalla lente mentre b la distanza dell'immagine dalla lente
f è la distanza focale
L'immagine di una lente divergente è sempre virtuale, perché i raggi divergono.
Inoltre è diritta e la distanza focale e la distanza dell'immagine dalla lente sono negative.
Il valore assoluto della distanza dell'immagine dalla lente b è sempre inferiore alla distanza dell'oggetto a:
Ne consegue che la dimensione dell'immagine è sempre più piccola della dimensione dell'oggetto, perché è dato da:
Chiariamo con un esempio:
Vediamo come varia l'immagine vista attraverso una lente convergente al variare della distanza dell'oggetto in relazione alla distanza focale della lente.
Per trovare l’immagine si possono disegnare due qualunque dei tre raggi del diagramma che partono dal punto superiore dell’oggetto. Il punto a destra della lente in cui si intersecano i tre raggi rifratti è l’immagine del punto da cui i raggi provengono.
Lente convergente: a>2f
L'immagine è reale, capovolta e scalata rispetto all'oggetto.
Questa disposizione è utilizzata nelle macchine fotografiche.
Lente convergente: a=2f
L'immagine è reale e della stessa dimensione dell'oggetto.
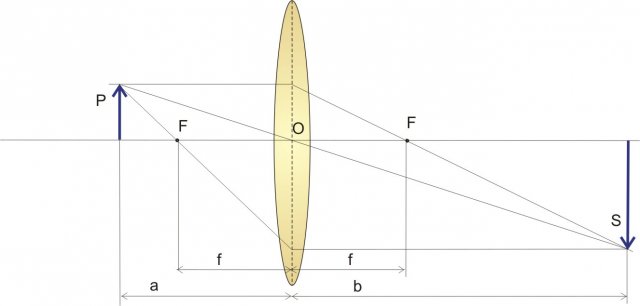
Lente convergente f < a < 2f
L'immagine è reale, più grande e capovolta.
Questa disposizione è usata nei proiettori.
Lente convergente: a=f
I raggi virtuali formano una immagine virtuale all'infinito, come ad esempio nelle lenti d'ingrandimento.
Lente convergente: a < f
L'immagine è virtuale, ingrandita e diritta.
Le lenti possono essere combinate insieme in modo da ottenere lenti composite. Possono essere montate insieme lenti entrambe convergenti, o divergenti o delle tue tipologie. L'accoppiamento di più lenti è usato nella costruzione di particolari strumenti ottici quali il microscopio o il telescopio per ottenere un ingrandimento maggiore di quello fornito da una singola lente.
Supponiamo ancora che le lenti siano sottili e siano congiunte.
Lenti combinate
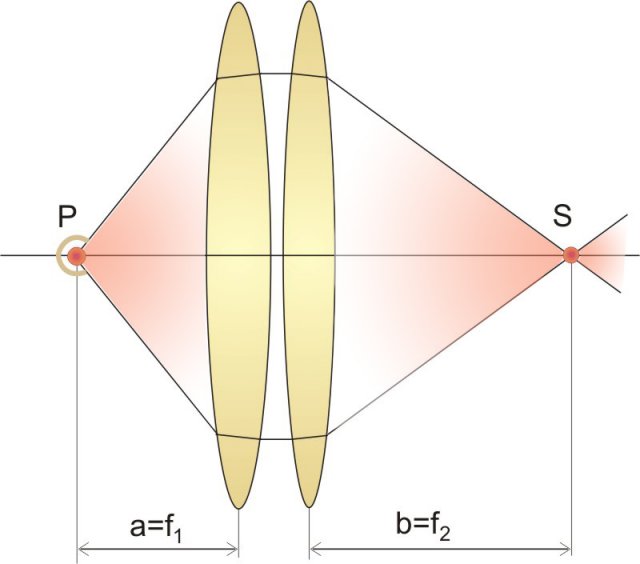
Consideriamo ad esempio due lenti convergenti combinate come illustrato nella figura precedente.
Applichiamo l'equazione delle lenti
L'espressione trovata ci dà la distanza focale di due lenti combinate.
Nel caso di lenti combinate il reciproco della distanza focale è pari alla somma dei reciproci delle distanze focali delle singole lenti:
Il reciproco della distanza focale è chiamato potere diottrico.
Il potere di rifrazione di una lente si misura con il potere diottrico della lente:
Tale grandezza dipende dalla distanza focale e quindi dal raggio della calotta sferica che costituisce la lente.
Il potere diottrico si misura con un'unità chiamata diottria.
Se si hanno più lenti (lenti combinate) si ha (come abbiamo visto nel paragrafo precedente):
Vale a dire, scrivendo la relazione in funzione del potere diottrico:
Gli occhiali sono un ulteriore esempio di lenti combinate.
