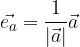Vettore spostamento
Consideriamo un punto A ed un secondo punto A'. Il vettore:
si chiama vettore spostamento.
Il modulo, la,direzione ed il verso del vettore spostamento sono quelli del vettore 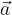
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Addizione e sottrazione di vettori
Addizione
Consideriamo due vettori 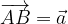 e
e 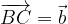 , come in Figura1.
, come in Figura1.
Si definisce somma o addizione tra i due vettori il vettore 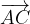 tale che:
tale che:
Se i due vettori sono disposti in modo da avere un punto di partenza comune (vedi Figura3), è possibile applicare la regola del parallelogramma. A partire dalla "testa" di ciascun vettore si traccia la parallela all'altro vettore. La somma dei vettori coincide con la diagonale del parallelogramma ottenuto.
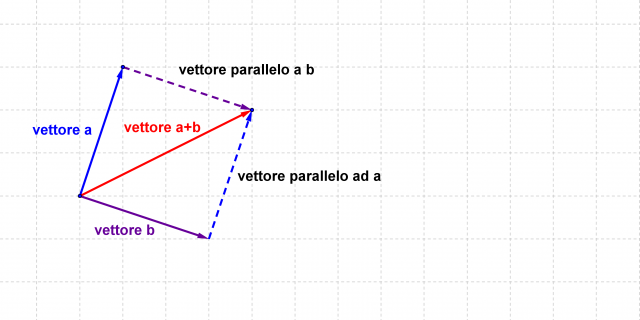
Figura3: Regola del parallelogramma
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà dell'addizione tra vettori
Dalle proprietà di addizione e sottrazione dei numeri reali si derivano le seguenti operazioni con i vettori:
L'addizione tra vettori gode della proprietà associativa:
valida per i vettori arbitrari 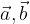 e
e 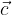 .
.
L'addizione tra vettori gode della proprietà commutativa:
valida per i vettori arbitrari 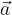 e
e 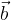 .
.
Elemento neutro nell'addizione o vettore zero
Sommando ad un vettore arbitrario il vettore 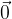 il vettore iniziale non cambia:
il vettore iniziale non cambia:
Si dice anche che il vettore 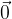 è l'elemento neutro nell'addizione tra vettori.
è l'elemento neutro nell'addizione tra vettori.
Legame tra Vettore opposto e vettore zero
Sommando ad un vettore il suo opposto si ottiene il vettore 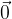 .
.
valida per il vettore arbitrario 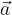 .
.
Sottrazione tra vettori
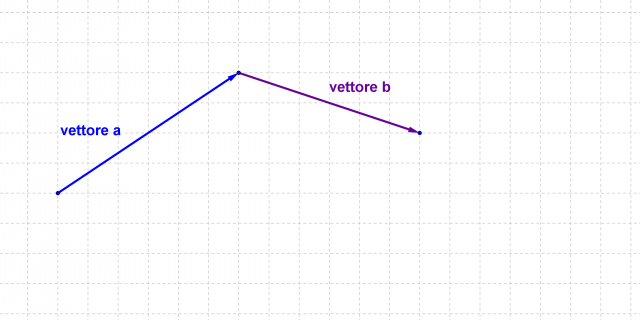
Siano dati i vettori 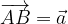 e
e 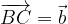 , come in Figura4.
, come in Figura4.
La sottrazione tra due vettori si ottiene sommando al primo vettore l'opposto del secondo vettore:
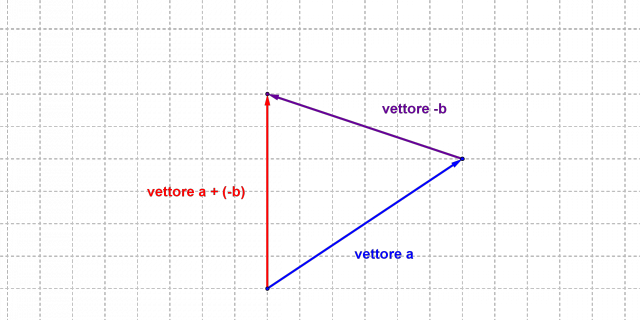
Graficamente possiamo notare che otteniamo il vettore opposto di 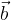 mantenendo la stessa dimensione e direzione, ma cambiando il verso della freccia (nel nostro esempio il vettore va da destra verso sinistra) e successivamente si applica la regola dell'addizione tra vettori (vedi Figura5).
mantenendo la stessa dimensione e direzione, ma cambiando il verso della freccia (nel nostro esempio il vettore va da destra verso sinistra) e successivamente si applica la regola dell'addizione tra vettori (vedi Figura5).
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Equazione vettoriale
E' una equazione in cui l'incognita è un vettore. In pratica si opera allo stesso modo di una equazione in cui l'incognita è un numero. Si pone uno dei vettori come vettore incognito e si scrivono le relazioni che permettono di trovare tale vettore.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Moltiplicazione di un vettore con uno scalare
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà della moltiplicazione tra un vettore ed uno scalare
Dalle proprietà di addizione e sottrazione tra numeri reali si derivano le seguenti operazioni tra vettori:
Dati due numeri reali k, l ed un vettore 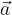 , la moltiplicazione gode della proprietà associativa:
, la moltiplicazione gode della proprietà associativa:
Dato un numero reale k e due vettori 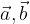 , la moltiplicazione gode della proprietà distributiva:
, la moltiplicazione gode della proprietà distributiva:
Dati due numeri reali k, l ed un vettore 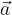 :
:
Unità nella moltiplicazione
Moltiplicando un qualunque vettore 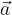 con il numero 1 il vettore non cambia:
con il numero 1 il vettore non cambia:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




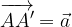
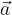
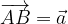 e
e 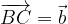 , come in Figura1.
, come in Figura1.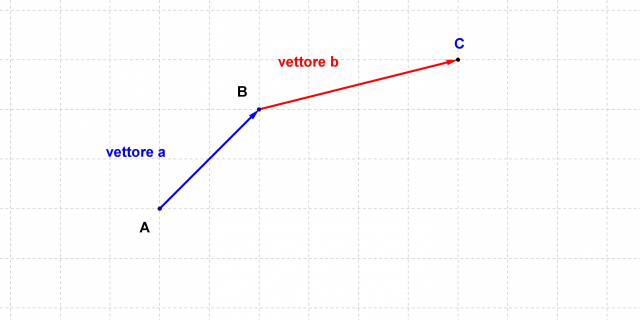
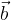
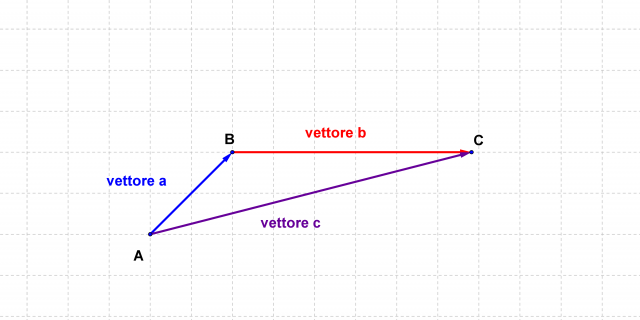
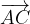 tale che:
tale che: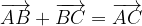

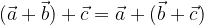
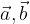 e
e 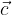 .
.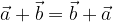
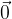 il vettore iniziale non cambia:
il vettore iniziale non cambia: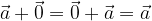
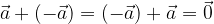
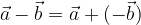
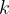 , diverso da zero, è il vettore
, diverso da zero, è il vettore 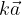 con le seguenti caratteristiche:
con le seguenti caratteristiche: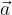 , se
, se 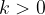
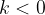
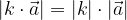
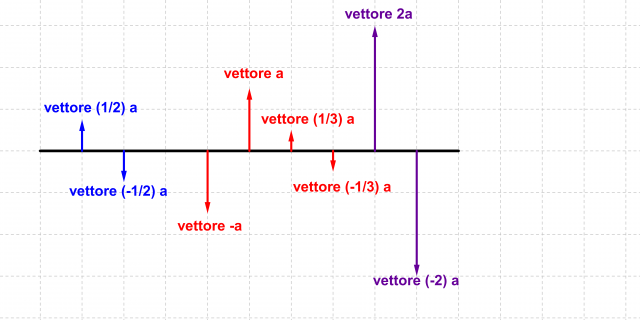
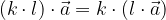
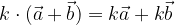
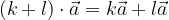
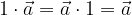
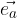 ) ha la stessa direzione e verso del vettore
) ha la stessa direzione e verso del vettore