Anche per i numeri complessi esistono le normali operazioni di somma, sottrazione, moltiplicazione, divisione ed elevamento a potenza. Vediamo come si definiscono tali operazioni.
Addizione di numeri complessi
Dati due numeri complessi:
Si definisce somma dei due numeri complessi il numero:
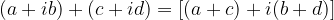
Il risultato è un numero complesso che ha come primo termine la somma dei primi termini dei numeri complessi addendi, e come secondo termine la somma dei secondi termini degli addendi. La definizione si applica anche nel caso di somma di tre o più numeri complessi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà della somma di numeri complessi:
Esiste l'elemento neutro e si indica con 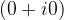 . Tale elemento si chiama numero complesso zero o nullo. Dato un qualunque numero complesso si ha che:
. Tale elemento si chiama numero complesso zero o nullo. Dato un qualunque numero complesso si ha che:
Il numero complesso opposto di 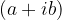 è:
è:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Dalla definizione di somma tra numeri complessi si può ricavare anche il concetto di differenza tra numeri complessi.
Si definisce differenza tra due numeri complessi 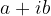 e
e 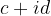 quel numero complesso che si ottiene sommando il primo numero con l'opposto del secondo.
quel numero complesso che si ottiene sommando il primo numero con l'opposto del secondo.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Moltiplicazione di numeri complessi
Dati due numeri complessi:
Si definisce prodotto dei due numeri complessi il numero
Nel caso di prodotto di tre numeri complessi, prima si effettua la moltiplicazione tra i primi due fattori, successivamente il risultato si moltiplica per il terzo. Tale definizione si applica anche nel caso di prodotto tra n numeri complessi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esiste l'elemento neutro e si indica con 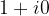 . Tale elemento si chiama numero complesso uno.
. Tale elemento si chiama numero complesso uno.
Dato un qualunque numero complesso 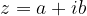 si ha che:
si ha che:
Reciproco di un numero complesso
Dato un numero complesso 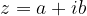 diverso da zero, esiste, ed è unico, l'opposto rispetto alla moltiplicazione: il numero complesso reciproco. E' quel numero complesso che moltiplicato per
diverso da zero, esiste, ed è unico, l'opposto rispetto alla moltiplicazione: il numero complesso reciproco. E' quel numero complesso che moltiplicato per 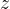 dà come prodotto 1.
dà come prodotto 1.
Dato un numero complesso 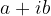 , diverso da zero, esiste ed è unico il suo reciproco, così definito:
, diverso da zero, esiste ed è unico il suo reciproco, così definito:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
In matematica una salita è anche una discesa: vediamo se la formula utilizzata per calcolare il reciproco è corretta, moltiplicando il numero di partenza con il reciproco ottenuto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Divisione di numeri complessi
Dalla definizione di reciproco si può ricavare anche il concetto di quoziente. Infatti, il quoziente tra due numeri complessi, altro non è che il prodotto del primo numero con il reciproco del secondo. Allo stesso modo in cui:
Allora, applicando la proprietà della moltiplicazione tra numeri complessi e del reciproco di un numero complesso si ottiene:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Potenze con esponente intero di numeri complessi
La definizione di potenza nel campo dei numeri reali può essere utilizzata anche nel campo dei numeri complessi.
Le regole relative alle potenze definite nel campo dei reali si possono applicare anche al caso complesso.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il campo complesso: ampliamento del campo reale
Operando questa definizione, è chiaro che l'eguaglianza gode delle proprietà riflessiva, simmetrica e transitiva.
Due numeri complessi sono diseguali se:
Nel campo dei numeri complessi non esistono i concetti di maggiore o minore. Infatti, i numeri complessi stanno su un piano e non su una retta!
Equazioni di secondo grado a una incognita nel campo complesso
Una equazione di secondo grado a coefficienti complessi ammette sempre soluzioni complesse che possono essere distinte se 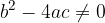 oppure coincidenti se
oppure coincidenti se 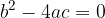 .
.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »






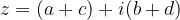
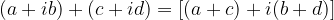
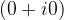 . Tale elemento si chiama numero complesso zero o nullo. Dato un qualunque numero complesso si ha che:
. Tale elemento si chiama numero complesso zero o nullo. Dato un qualunque numero complesso si ha che: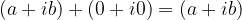
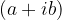 è:
è: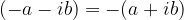
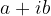 e
e 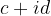 quel numero complesso che si ottiene sommando il primo numero con l'opposto del secondo.
quel numero complesso che si ottiene sommando il primo numero con l'opposto del secondo.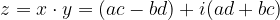
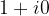 . Tale elemento si chiama numero complesso uno.
. Tale elemento si chiama numero complesso uno.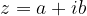 si ha che:
si ha che: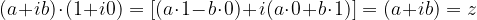
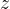 dà come prodotto 1.
dà come prodotto 1.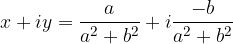
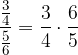
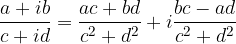
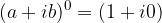 <=>
<=> 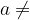 0 e
0 e 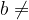 0.
0.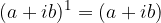
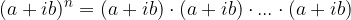 se
se 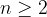
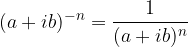 se
se 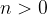 e
e 

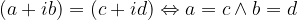
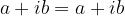
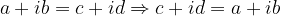
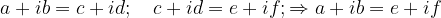
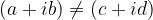
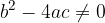 oppure coincidenti se
oppure coincidenti se 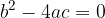 .
.


