Si chiama proposizione un'espressione linguistica per la quale ha senso domandarsi se essa è vera (V) o falsa (F). Non sono proposizioni le interrogazioni, gli imperativi e le frasi soggettive. Una proposizione può essere atomica o molecolare. Una proposizione è atomica se risulta composta dal soggetto e dal predicato. Una proposizione si dice molecolare se è composta da una o più proposizioni atomiche
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Assiomi della logica
La logica è regolata da tre principi aristotelici
Ogni proposizione è identica a stessa( ha lo stesso valore di verità).
Ogni proposizione non può essere sia vera che falsa.
Ogni proposizione o è vera o è falsa.
Operatori logici
Le varie proposizioni logiche possono essere concatenate tra di loro per formare delle espressioni logiche complesse tramite gli operatori logici. Vediamo adesso quali sono questi operatori e i loro rispettivi significati.
La negazione NOT
La negazione NOT è l'operazione che applicata a una proposizione p restituisce il contrario di p. Indichiamo la negazione di p in questo modo.
Se p è vera allora 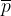 è falsa;
è falsa;
Se p è falsa allora 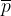 è vera;
è vera;
Rappresentiamo i due punti precedenti una tabella, detta tabella di verità:
Pertanto se la proposizione è vera la sua negazione è falsa. E viceversa
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La doppia Negazione
La DOPPIA NEGAZIONE è l'operazione che applicata a una proposizione p restituisce il suo originale valore di verita. Indichiamo la doppia negazione di p in questo modo 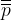 .
.
Se p è vera allora 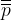 è vera
è vera
Se p è falsa allora 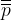 è falsa
è falsa
Rappresentiamo i due punti precedenti una tabella, detta tabella di verità:
Pertanto se la proposizione è vera la sua doppia negazione è anche essa vera. E viceversa
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La congiunzione AND
La congiunzione AND è un operatore binario in quanto coinvolge sempre due proposizioni logiche. La indichiamo con AND oppure con il simbolo 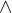 . Vediamo la sua tabella di verità:
. Vediamo la sua tabella di verità:
La proposizione ottenuta dalla congiunzione di p e di q è vera se entrambe le proposizioni che la compongono risultano essere vere. In casa contrario essa risulta essere falsa.
Vediamo un esempio per fissare il concetto
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La disgiunzione OR
La disgiunzione OR è un operatore binario . La indichiamo con OR oppure con il simbolo 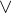 . Esaminiamo la sua tabella di verità:
. Esaminiamo la sua tabella di verità:
La proposizione ottenuta dalla disgiunzione di p e di q è vera se almeno una delle due proposizioni che la compongono risultano essere vere. Pertanto risulta essere falsa solo quando entrambe le proposizioni sono false.
Vediamo un esempio per fissare il concetto
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La disgiunzione XOR
La disgiunzione esclusiva XOR è un operatore binario. Tale operatore è molto simile all'OR, tranne nel caso in cui gli operatori assumono lo stesso valore. Esaminiamo la tabella di verità:
La disgiunzione esclusiva
La proposizione ottenuta dalla disgiunzione esclusiva di p e di q è vera quando le due proposizioni coinvolte assumono un diverso valore di verità, mentre è falsa quando assumono lo stesso valore.
Vediamo un ulteriore esempio
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Espressioni con i connettivi logici
Le operazioni appena illustrate di NOT, AND, OR e XOR possono essere usate per costruire delle proposizioni complesse utilizzando due o più proposizioni semplici. Di queste proposizioni è possibile costruire la rispettiva tabella di verità composta da tante colonne quante sono le proposizioni che compongono l'espressione , e da una unica colonna finale contente il valore di verità della espressione cosi ottenuta.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
L'espressione è composta da tre tre proposizione( p, q, r ) e dunque la tabella presenta tre colonne , più una aggiuntiva che riporta il valore di verità dell'espressione. Ovviamente tale valore dipende dai valori di verità attribuiti alle singole proposizioni che compongono l'espressione.
Implicazione materiale
Si definisce IMPLICAZIONE MATERIALE di due proposizioni p e q la nuova proposizione che indichiamo con la seguente simbologia:
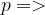 q
q
Ilustriamo la tabella di verita:
Una proposizione ottenuta tramite l'implicazione materiale è dunque falsa solo quando la proposizione p è vera mentre la q risulta essere falsa. Stabilire , da un punto di vista matematica, che l'implicazione è vera, è equivalente al seguente enunciato:
L'ipotesi p è sufficiente per la tesi q.
Vediamo un esempio per fissare il concetto
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Doppia implicazione
Se valgono entrambe le seguenti proprietà :
Allora esiste un legame di doppia implicazione tra le proposizione p e q. L'operatore logico che esprime ciò è invece il seguente:
In altre parole si dice che l'ipotesi p è una condizione necessaria e sufficiente per la tesi q. Vediamo la tabella di verità.
Una proposizione ottenuta tramite l'operatore di doppia implicazione è vera quando la tesi(p) e l'ipotesi(q) risultano essere entrambe vere o entrambe false.
Vediamo un ulteriore esempio per fissare il concetto
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
I procedimenti logici (1) e (4) in geometria vengono chiamati metodi di Dimostrazione diretta e Ragionamento per assurdo.
Tautologia
Si definisce tautologia una proposizione logica sempre VERA , cioè soddisfatta per qualsiasi valore di verità assunto dalle espressioni che la compongono.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
La proposizione 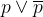 è dunque sempre vera. Fissiamo il concetto di tautologia con un esempio
è dunque sempre vera. Fissiamo il concetto di tautologia con un esempio
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





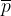 è falsa;
è falsa;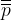 .
.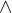 . Vediamo la sua tabella di verità:
. Vediamo la sua tabella di verità: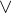 . Esaminiamo la sua tabella di verità:
. Esaminiamo la sua tabella di verità: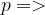 q
q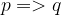

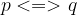
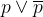 è dunque sempre vera. Fissiamo il concetto di tautologia con un esempio
è dunque sempre vera. Fissiamo il concetto di tautologia con un esempio


