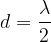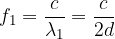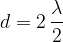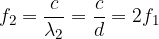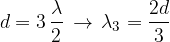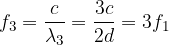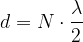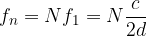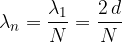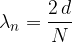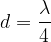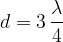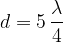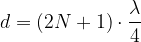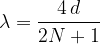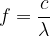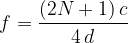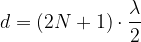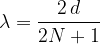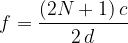Nelle onde trasversali le particelle oscillano perpendicolarmente alla direzione di propagazione.
Questo tipo di onde si genera, ad esempio, nelle corde di una chitarra o di un violino, nella membrana di un tamburo o sulle barre di legno di uno xilofono.
Esempi di strumenti: chitarra, kalimba, xilofono
La figura rappresenta tre diversi strumenti nei quali l'elemento vibrante (le corde, le linguette e le barrette) generano onde trasversali. Ciò che li diversifica è il modo in cui gli elementi sono fissati: nella chitarra le corde sono fissate a entrambe le estremità, nel kalimba sono a un'estremità, nello xilofono sono libere.
Quando pizzichiamo una corda creiamo una perturbazione che si propaga fino a non finisce la corda o finché la perturbazione non trova un ostacolo (il punto in cui la corda è fissata). A quel punto l'oscillazione viene riflessa e torna indietro.
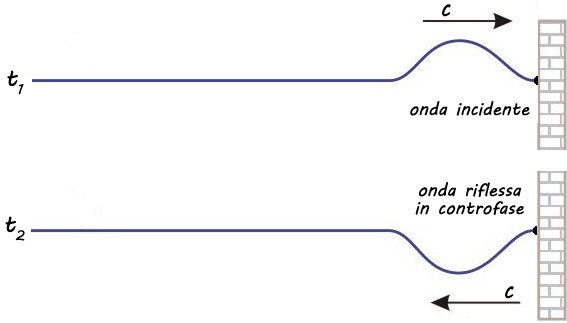
Riflessione di un'onda su una corda fissata a un'estremità
Se la corda è fissata alla parete come mostrato in figura, l'onda riflessa ha la cresta dove prima aveva il ventre e viceversa, si dice che l'onda è in opposizione di fase.
Nel caso in cui la corda sia fissata a delle pulegge mobili sia ha che le estremità della corda possano seguire le oscillazioni.
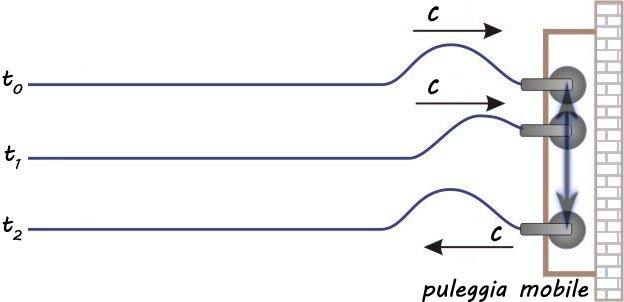
La corda è fissata a una puleggia mobile
Le onde stazionarie si formano perché sulla corda si propagano onde identiche che viaggiano in versi opposti e si sommano per il principio di sovrapposizione.
Si chiamano stazionarie perché, come suggerisce il nome, non si muovono in nessuna direzione.
onda trasversale
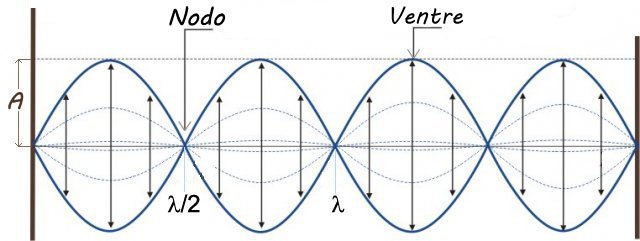
Osserviamo che nelle onde stazionarie ci sono alcuni punti particolari, chiamati nodi e ventri. I nodi sono i punti in cui non c’è vibrazione, mentre i ventri sono i punti in cui l’ampiezza è massima.
A un certo valore della frequenza corrisponde un modo (vale a dire una "forma" con un certo numero di nodi e ventri) dell'onda stazionaria. Queste frequenze formano una serie, chiamata serie armonica.
La frequenza minore è la prima armonica o frequenza fondamentale e corrisponde alla frequenza minima dell’onda raggiungibile nella corda. In questo caso la corda ha due nodi e un ventre.
Le frequenze successive sono multipli interi della frequenza fondamentale e sono chiamate seconda, terza, quarta, ... armonica.
Il numero dell’armonica (prima, seconda, terza ecc.) corrisponde al numero di ventri nel modo normale dell’onda stazionaria.
La frequenza fondamentale (o di base) di una corda tesa dipende sia dalla velocità delle onde, sia dalla lunghezza della corda e sia da come sono fissate le estremità.
La corda è fissata a entrambe le estremità, per far nascere delle vibrazioni viene pizzicata con un plettro.
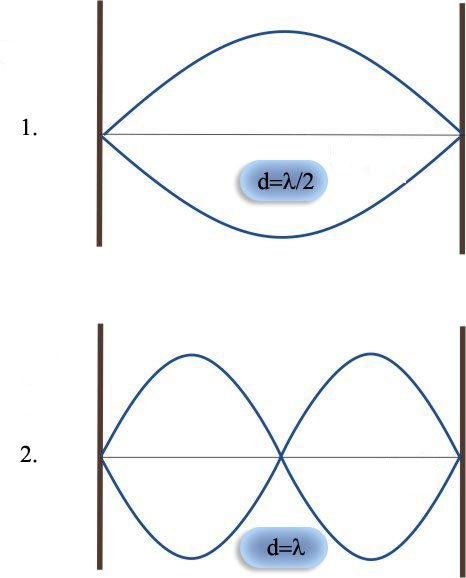
Corda lunga d fissata alle estremità
Nella parte superiore della figura vediamo la corda che vibra con la sua frequenza fondamentale, mentre nella parte inferiore la corda che oscilla con la frequenza della seconda armonica.
La prima armonica della corda si ha quando la lunghezza della corda d è uguale alla metà della lunghezza d'onda:
la frequenza della prima armonica quindi è:
Esistono anche altre armoniche oltre la prima, ad esempio si ha la seconda armonica quando:
e la frequenza corrispondente vale:
Vediamo anche il caso della terza armonica:
e la frequenza:
In generale, nasce un'onda stazionaria quando la lunghezza della corda d è:
in termini di frequenza:
o, in termini di lunghezza d'onda:
dove N assume valori naturali interi (N = 1, 2, 3, ....). Notiamo quindi che un’armonica contiene sempre mezza lunghezza d’onda in più della precedente.
La lunghezza d'onda di un'onda stazionaria in una corda fissata ad entrambe le estremità è:
dove N indica le armoniche (multipli della frequenza fondamentale) e d è la lunghezza della corda.
La frequenza:
Consideriamo invece il kalimba, in questo caso le linguette metalliche funzionano come delle corde fissate a una sola estremità.
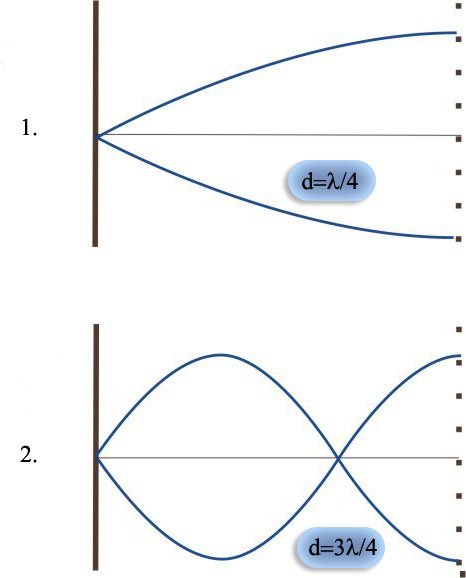
La linguetta è fissata a una estremità.
Dalla figura osserviamo che le oscillazioni della lunghezza d della corda è pari ad un quarto della lunghezza d'onda:
Si ottiene la prima armonica quando:
la seconda frequenza armonica quando:
ecc ecc... In generale, si genera un'onda stazionaria quando la lunghezza d :
o, in termini di lunghezza d'onda:
dove N assume i valori (N = 0, 3, 5, ....).
La lunghezza d'onda di un'onda stazionaria che si propaga in una corda con un'estremità libera è:
dove N indica le armoniche e d la lunghezza della corda.
Calcoliamo anche la frequenza:
Sostituiamo l'espressione della lunghezza d'onda:
Quando N = 0, si ottiene la frequenza fondamentale, se N = 3 si ottiene la prima armonica, e così via.
Consideriamo un altro tipo di strumento, lo xilofono. In questo strumento l'elemento vibrante sono delle barrette di legno sostenute sul telaio da dei piccoli sostegni elastici lasciando le estremità libere di oscillare. Le perturbazioni vengono generate battendo con dei martelletti sulle barrette.
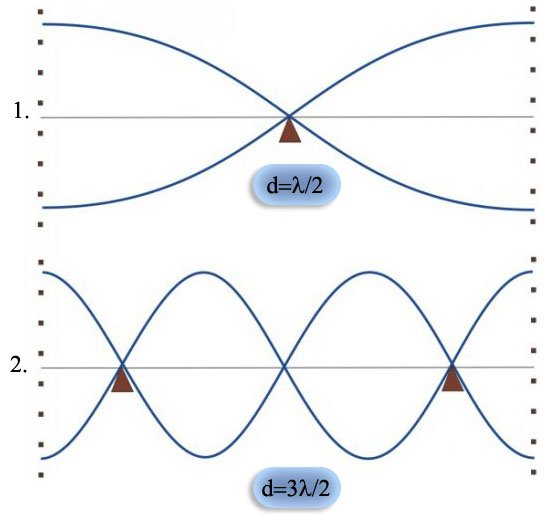
Barretta libera alle estremità sostenuta da sostegni elastici
Nella parte superiore dell'immagine è rappresentata la frequenza fondamentale, nella parte inferiore la seconda armonica. Il triangolo indica la posizione in cui la barretta può essere sostenuta (cioè in corrispondenza dei nodi).
In generale nasce un'onda stazionaria quando la lunghezza della corda d sarà:
o, in termini di lunghezza d'onda, quando:
dove N può essere zero o un numero naturale dispari (N = 0, 3, 5, ....)
La lunghezza d'onda dell'onda stazionaria di una corda libera è pari a:
dove N indica le armoniche armoniche (cioè i multipli della frequenza fondamentale) mentre d è la la lunghezza della corda.
Ricaviamo anche per questo caso la frequenza:
nella quale sostituiamo l'espressione della lunghezza d'onda appena ricavata:
Se N=0, otteniamo la frequenza fondamentale.
