Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





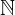 si possono dividere in tre gruppi in base ai loro divisori:
si possono dividere in tre gruppi in base ai loro divisori: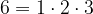
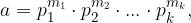
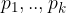 sono numeri primi e
sono numeri primi e 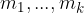 sono numeri naturali.
sono numeri naturali.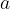 .
.