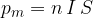Corrente elettrica in campo magnetico
Immaginiamo una spira quadrata immersa in un campo magnetico B costante come in figura. Quando questa viene percorsa da corrente elettrica gli elettroni, muovendosi all'interno di un campo magnetico, risentono della forza di Lorentz come visto nel paragrafo Forza magnetica su cariche elettriche. Solo i tratti della spira perpendicolari al flusso del campo magnetico (b) risentiranno di una forza F che genererà quindi sulla spira un momento proporzionale alla largezza a/2 della stessa.
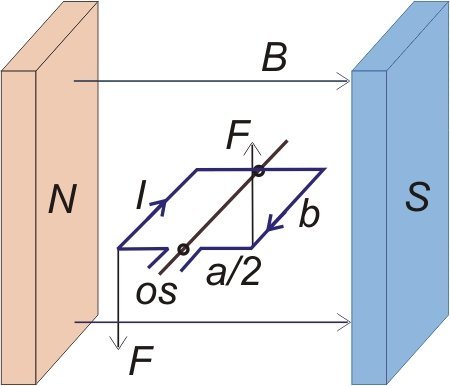
Forze di coppia su una spira immersa in un campo magnetico
Il momento totale agente sulla spira sarè quindi dato da:
Se modifichiamo l'inclinazione della nostra spira la lunghezza del braccio del momento diminuirà in funzione dell'angolo. Di conseguenza, diminuirà il momento stesso.
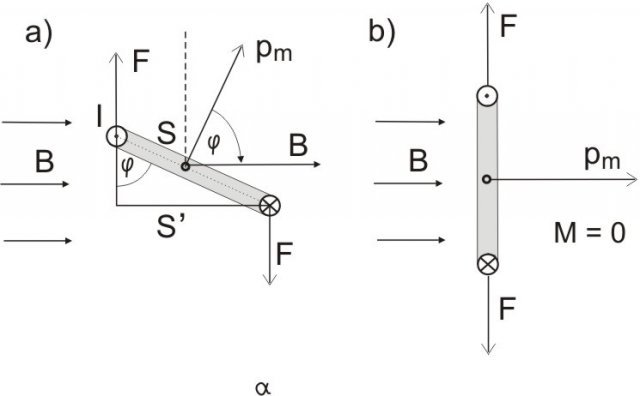
Se la spira è libera di ruotare il momento si annulla quando questa è perpendicolare al flusso magnetico
La figura posta sopra mostra la dinamica di una spira, vista dall'alto, soggetta ad un campo magnetico. Il cerchio con la croce sta ad indicare che la corrente esce quel punto, per andare verso il cerchio con il punto al centro.
Si chiama momento magnetico il vettore 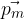 .
.
Il suo modulo è pari al prodotto tra la corrente che attraversa il circuito e la superficie delimitata da esso:
La direzione è perpendicolare al piano formato dalla spira. Il verso è individuato dal pollice della mano destra quando le dita si avvolgono nel verso della corrente.
A questo punto possiamo definire il momento meccanico della spira, che è in modulo:
Dove 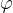 è l'angolo formato dal versore del momento magnetico e il campo magnetico.
è l'angolo formato dal versore del momento magnetico e il campo magnetico.
Il momento magnetico ha valore massimo quando 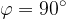 . Ha invece valore nullo quando
. Ha invece valore nullo quando 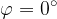 , ossia quando la spira è parallela al campo magnetico
, ossia quando la spira è parallela al campo magnetico
Bobina immersa in un campo magnetico
Al posto di una singola spira possiamo immergere in un campo magnetico anche una bobina, ossia un insieme di spire sovrapposte. Generalizzando quanto abbiamo trovato nei paragrafi precedenti possiamo dire che non conta la forma della bobina ma solo la sezione trasversale S, il numero di avvolgimenti e l'angolo tra l'asse della spira e le linee del campo magnetico.
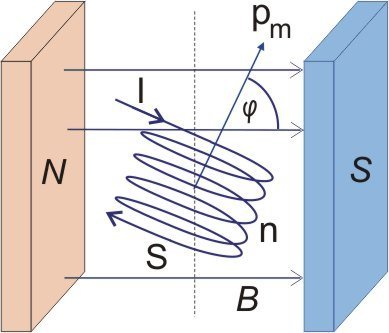
Bobina immersa in un campo magnetico
Il momento magnetico a cui la bobina è sottoposta è n volte maggiore rispetto a quello della singola spira:
La coppia finale è quindi data da:





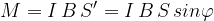

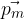 .
.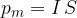
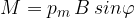
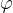 è l'angolo formato dal versore del momento magnetico e il campo magnetico.
è l'angolo formato dal versore del momento magnetico e il campo magnetico.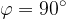 . Ha invece valore nullo quando
. Ha invece valore nullo quando 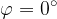 , ossia quando la spira è parallela al campo magnetico
, ossia quando la spira è parallela al campo magnetico