Libri personalizzati
Scuole superiori
Meccanica
Termodinamica
Oscillazioni e onde
Elettromagnetismo
Libri degli insegnanti





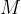 che abbiamo fissato, man mano che la variabile x si avvicina ad un determinato punto a, ovvero possiamo scrivere:
che abbiamo fissato, man mano che la variabile x si avvicina ad un determinato punto a, ovvero possiamo scrivere: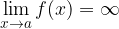
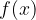 definita in un intorno del punto
definita in un intorno del punto 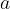 escluso il punto stesso, si dice che:
escluso il punto stesso, si dice che: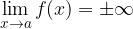
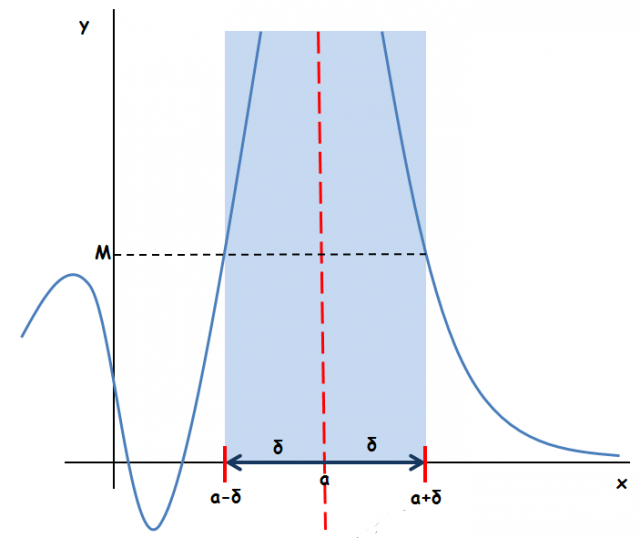
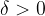 , tale che, per ogni x che appartiene all'intorno di a vale la condizione:
, tale che, per ogni x che appartiene all'intorno di a vale la condizione: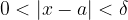
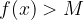 per limite =
per limite =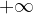
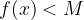 nel caso di limite =
nel caso di limite = 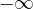
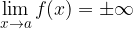
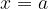 .
.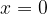 rappresenta un asintoto per la funzione stessa.
rappresenta un asintoto per la funzione stessa.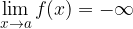
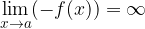
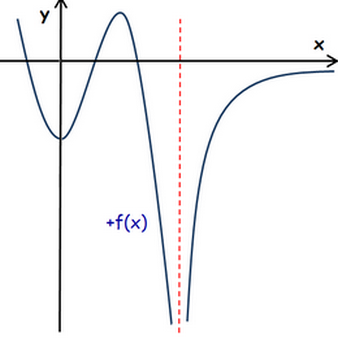

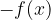 ha un limite infinito positivo
ha un limite infinito positivo


