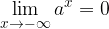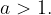Con un limite all'infinito possiamo descrivere il comportamento di una funzione lontano dall'origine degli assi, ovvero quando la variabile indipendente 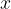 assume valori positivi o negativi infinitamente grandi.
assume valori positivi o negativi infinitamente grandi.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Definizione di limite all'infinito
Per comprendere la definizione di limite all'infinito, rivediamo i seguenti concetti:
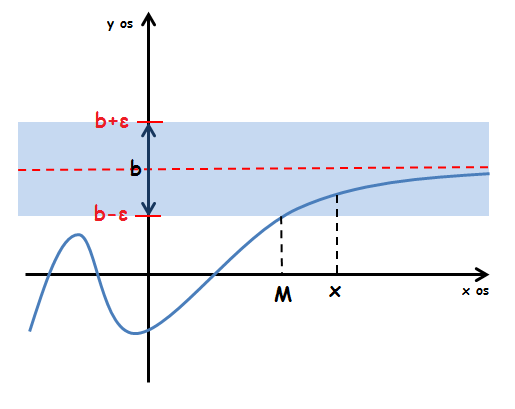
Fissiamo un valore arbitrario 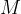 , sufficientemente grande, sull'asse delle x, tale che per qualunque valore di x maggiore di questo estremo fissato, i valori che assume la funzione
, sufficientemente grande, sull'asse delle x, tale che per qualunque valore di x maggiore di questo estremo fissato, i valori che assume la funzione 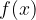 ricadano nell'intorno del punto b fissato in precedenza e, quanto più x si allontana da M, tanto più f(x) si avvicina al valore b.
ricadano nell'intorno del punto b fissato in precedenza e, quanto più x si allontana da M, tanto più f(x) si avvicina al valore b.
Adesso possiamo enunciare la definizione di limite della funzione f(x) all'infinito:
se, fissato un numero 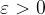 , è possibile determinare un numero
, è possibile determinare un numero 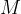 , tale che, per ogni x per cui vale:
, tale che, per ogni x per cui vale:
Possiamo rappresentare graficamente quanto detto nel modo seguente:
Limite all'infinito di funzioni simmetriche rispetto all'asse delle ordinate
Consideriamo la funzione 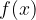 . Se abbiamo che:
. Se abbiamo che:
Quando i grafici di due funzioni sono simmetrici rispetto all'asse delle ordinate, varrà dunque la seguente uguaglianza:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Limite all'infinito delle funzioni razionali
Consideriamo una funzione razionale del tipo:
potranno verificarsi i seguenti casi nei quali considereremo che il grado del polinomio al numeratore e al denominatore differiscono di una sola unità. Poniamo questa condizione per il fatto che considereremo solo funzioni che abbiano asintoti lineari.
Caso 1: Polinomio al numeratore con grado inferiore del denominatore
con x che tende all'infinito, il denominatore tenderà a valori infinitamente grandi più velocemente del numeratore, pertanto il rapporto tenderà ad essere infinitamente piccolo.
ovvero la funzione ha per asintoto orizzontale l'asse delle ascisse:
Caso 2: Polinomio al numeratore e denominatore di stesso grado
in cui 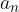 e
e 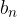 sono i coefficienti di grado massimo dei due polinomi.
sono i coefficienti di grado massimo dei due polinomi.
è quindi asintoto orizzontale della funzione.
Caso 3: Polinomio al numeratore con grado superiore del denominatore
Il numeratore tenderà verso valori infinitamente grandi più velocemente del denominatore e quindi anche il quoziente tenderà a valori infinitamente grandi:
Ciò vuol dire che la funzione può avere un asintoto obliquo, poiché quanto più grande è il valore di 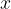 , tanto più la funzione assume valori che si avvicinano a quelli della funzione lineare
, tanto più la funzione assume valori che si avvicinano a quelli della funzione lineare 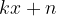 .
.
L'equazione lineare 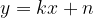 è l'equazione dell'asintoto obliquo che possiamo calcolare come segue:
è l'equazione dell'asintoto obliquo che possiamo calcolare come segue:
Equazione dell'asintoto obliquo
Consideriamo la funzione razionale:
per trovare l'equazione dell'asintoto obliquo, dividiamo il numeratore 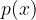 per il denominatore
per il denominatore 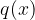 . Otterremo:
. Otterremo:
dove 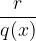 è il resto della divisione. Poiché però sappiamo che x tende a valori infinitamente grandi, il resto tenderà a zero.
è il resto della divisione. Poiché però sappiamo che x tende a valori infinitamente grandi, il resto tenderà a zero.
Ne consegue che il rapporto del numeratore e denominatore ci dà proprio l'equazione dell'asintoto obliquo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Limite all'infinito di funzioni esponenziali
Ricordiamo che una funzione esponenziale è una funzione del tipo:
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Quanto abbiamo visto nell'esempio si verifica poiché abbiamo considerato una funzione esponenziale la cui base è un numero decimale compreso tra 0 e 1. Quanto maggiore è l'esponente, tanto minore è il valore della potenza, se l'esponente è positivo. Ne consegue che, quanto visto, dipende dal valore di infinito a cui si fa tendere la x, ovvero se si fa tendere x a 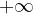 o a
o a 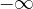 .
.
Pertanto l'affermazione di cui sopra si applica solo ai seguenti casi:
Il limite di una funzione esponenziale è:
se 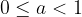 o:
o:
se 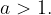




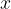 assume valori positivi o negativi infinitamente grandi.
assume valori positivi o negativi infinitamente grandi.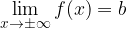
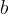 sull'asse delle ordinate, ovvero fissiamo un numero arbitrario positivo e sufficientemente piccolo
sull'asse delle ordinate, ovvero fissiamo un numero arbitrario positivo e sufficientemente piccolo  tale che si abbia un intervallo aperto di estremi
tale che si abbia un intervallo aperto di estremi 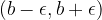 . Tale intervallo è l'intorno del punto
. Tale intervallo è l'intorno del punto 
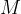 , sufficientemente grande, sull'asse delle x, tale che per qualunque valore di x maggiore di questo estremo fissato, i valori che assume la funzione
, sufficientemente grande, sull'asse delle x, tale che per qualunque valore di x maggiore di questo estremo fissato, i valori che assume la funzione 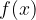 ricadano nell'intorno del punto b fissato in precedenza e, quanto più x si allontana da M, tanto più f(x) si avvicina al valore b.
ricadano nell'intorno del punto b fissato in precedenza e, quanto più x si allontana da M, tanto più f(x) si avvicina al valore b.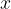 tendente all'infinito, ha per limite il numero
tendente all'infinito, ha per limite il numero 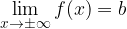
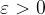 , è possibile determinare un numero
, è possibile determinare un numero 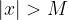
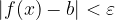
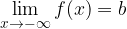
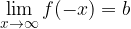
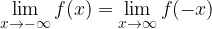
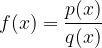
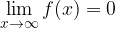
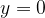
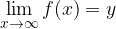
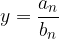
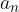 e
e 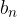 sono i coefficienti di grado massimo dei due polinomi.
sono i coefficienti di grado massimo dei due polinomi.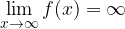
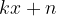 .
.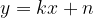 è l'equazione dell'asintoto obliquo che possiamo calcolare come segue:
è l'equazione dell'asintoto obliquo che possiamo calcolare come segue: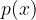 per il denominatore
per il denominatore 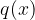 . Otterremo:
. Otterremo: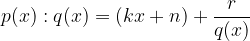
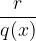 è il resto della divisione. Poiché però sappiamo che x tende a valori infinitamente grandi, il resto tenderà a zero.
è il resto della divisione. Poiché però sappiamo che x tende a valori infinitamente grandi, il resto tenderà a zero.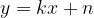
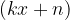 o, in altre parole, tanto minore diventa la differenza tra
o, in altre parole, tanto minore diventa la differenza tra 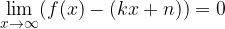
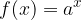
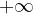 o a
o a 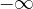 .
.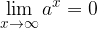
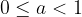 o:
o: