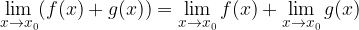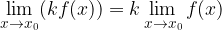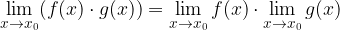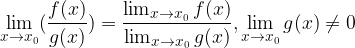Alcune volte, per un dato valore di x, la funzione non è definita o sembra non definita. Per capire la differenza tra le due possiamo, con lo studio dei limiti, cercare di dare a questi valori una rappresentazione, studiando cosa succede per valori quanto più "vicini" al punto problematico.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Intorno di un punto
Poiché abbiamo parlato di valori vicini al punto 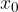 , per comprendere cos'è il limite di una funzione, dobbiamo innanzitutto definire il concetto fondamentale di intorno di un punto.
, per comprendere cos'è il limite di una funzione, dobbiamo innanzitutto definire il concetto fondamentale di intorno di un punto.
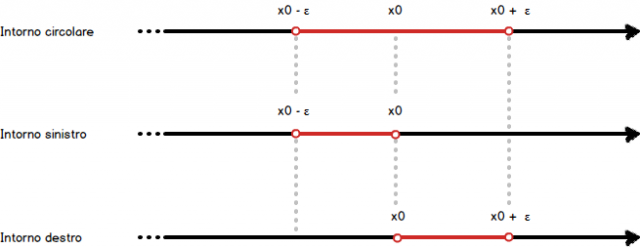
L'intorno di un punto 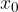 è un insieme aperto contenente il punto
è un insieme aperto contenente il punto 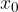 .
.
Ciò significa che l'ampiezza dell'intervallo sarà 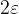 e che i suoi estremi sono:
e che i suoi estremi sono: 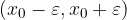 .
.
Generalmente un intorno è indicato con 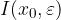 e in seguito nel capitolo lo chiameremo in questo modo:
e in seguito nel capitolo lo chiameremo in questo modo:
Definizione di limite di una funzione
Vediamo ora un esempio che possa chiarire il concetto di limite.
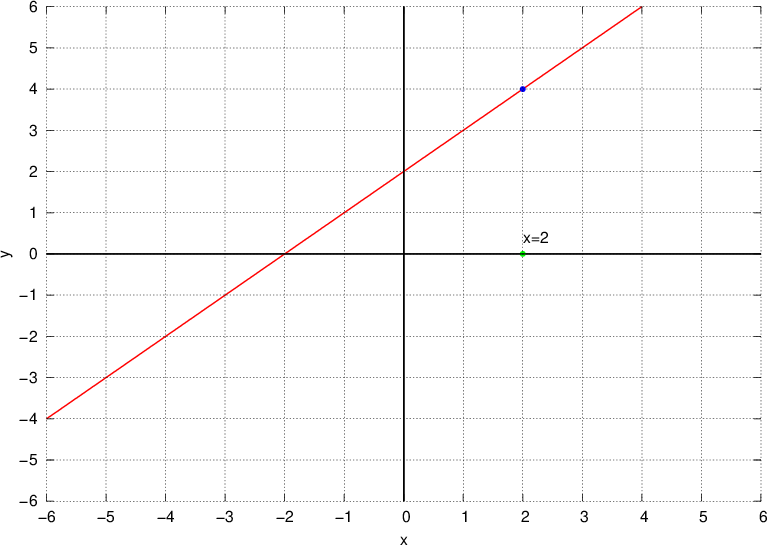
Consideriamo di nuovo la funzione:
Come possiamo osservare la funzione non è definita per x = 2 in quanto il denominatore dev'essere in ogni caso diverso da 0.
Possiamo tuttavia calcolare i valori più prossimi a 2 sia per eccesso che per difetto ovvero considerare il suo intorno circolare.
Per valori più piccoli di 2.
Per valori più grandi di 2.
Osservando le due tabelle notiamo che più x si avvicina a 2, più i valori di f(x) si avvicinano a 4.
Possiamo anche affermare, in altre parole, che quanto più x si avvicina a 2, tanto meno i valori di f(x) distano dal valore 4: la differenza tra la funzione f(x) e il valore 4 diminuisce rispetto ad un valore arbitrario positivo  che rappresenta l'ampiezza dell'intorno di 4:
che rappresenta l'ampiezza dell'intorno di 4:
Vediamo dunque cosa succede quando tale differenza è minore di 
Come possiamo vedere, i valori di f(x) differiscono da 4 di un valore  , ovvero appartengono a un intorno di 4, purchè x sia sufficientemente vicino a 2, ovvero appartenga a un intorno di 2.
, ovvero appartengono a un intorno di 4, purchè x sia sufficientemente vicino a 2, ovvero appartenga a un intorno di 2.
Possiamo scrivere quanto affermato nel seguente modo:
se, fissato un numero 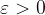 , è possibile determinare un numero
, è possibile determinare un numero 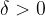 , tale che, per ogni x che appartiene all'intorno vale la condizione:
, tale che, per ogni x che appartiene all'intorno vale la condizione:
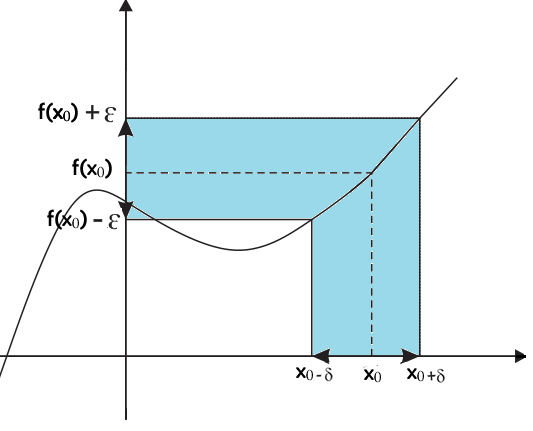
Visto in forma grafica risulta:
I valori di 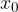 e
e 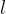 definiscono il limite della funzione.
definiscono il limite della funzione.
Tipologie di limite
In base ai valori che possono assumere 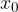 e
e 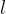 , possiamo avere i seguenti tipi di limite:
, possiamo avere i seguenti tipi di limite:
limite finito in un punto:
limite infinito in un punto:
limite finito per x tendente all'infinito:
limite infinito per x tendente all'infinito:
Limite finito di una funzione per x che tende a un valore finito
Come abbiamo visto, può verificarsi che in un determinato punto, una funzione non sia definita. Nonostante ciò è possibile studiare il comportamento della funzione in tale punto, quanto più ci si avvicina la variabile indipendente x.
Vediamo un esempio di funzione non definita in un punto, ma per la quale esiste un limite finito l.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Operazioni sui limiti
Nel calcolo dei limiti di una funzione, valgono le seguenti regole:
1. Il limite di una somma equivale alla somma dei limiti:
2. Il limite del prodotto tra una costante e una funzione equivale al prodotto della costante per il limite della funzione:
3. Il limite di un prodotto è uguale al prodotto dei limiti:
4. Il limite di un quoziente equivale al quoziente dei limiti, purché il limite della funzione al denominatore non sia nullo:





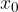 , per comprendere cos'è il limite di una funzione, dobbiamo innanzitutto definire il concetto fondamentale di intorno di un punto.
, per comprendere cos'è il limite di una funzione, dobbiamo innanzitutto definire il concetto fondamentale di intorno di un punto.
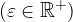 .
.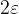 e che i suoi estremi sono:
e che i suoi estremi sono: 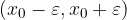 .
.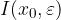 e in seguito nel capitolo lo chiameremo in questo modo:
e in seguito nel capitolo lo chiameremo in questo modo: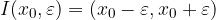
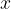 , esso apparterrà all'intorno di
, esso apparterrà all'intorno di 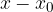 è minore di
è minore di 
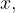 tali che la loro distanza da
tali che la loro distanza da 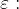
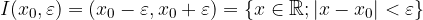
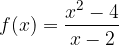
 che rappresenta l'ampiezza dell'intorno di 4:
che rappresenta l'ampiezza dell'intorno di 4: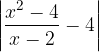
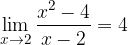
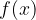 una funzione definita in un intorno del punto
una funzione definita in un intorno del punto 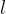 è il limite della funzione
è il limite della funzione 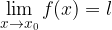
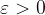 , è possibile determinare un numero
, è possibile determinare un numero 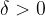 , tale che, per ogni x che appartiene all'intorno vale la condizione:
, tale che, per ogni x che appartiene all'intorno vale la condizione: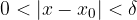
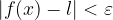
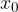 e
e 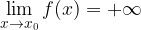
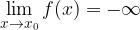
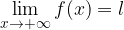
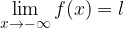
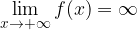
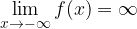
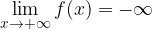
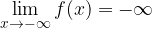
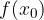 che assume la funzione in quel punto.
che assume la funzione in quel punto.