Prerequisiti
Ora definiremo i componenti strutturali che caratterizzano un circuito (o rete) elettrico in corrente continua e vedremo in che senso e come si possa risolvere.
Topologia delle reti elettriche
Prima di proseguire con la trattazione dobbiamo metterci d'accordo su alcuni termini che utilizzeremo.
Analisi delle reti elettriche
In linea di principio risolvere un circuito elettrico significa determinare la corrente circolante e la tensione applicata ad ogni suo ramo.
Ci sono varie ragioni per voler fare ciò ed una di esse è la possibilità di analizzare il comportamento del circuito elettrico considerato ossia di conoscere in anticipo tensione e corrente in ogni suo punto e stimare la potenza che andrà ad assorbire.
Nel nostro caso vedremo circuiti in corrente continua formati da resistori e generatori ideali: l'analisi richiederà di calcolare coppie tensione-corrente (I,V) per ogni resistore e generatore del circuito.
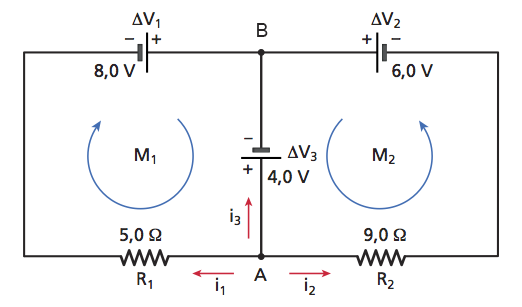
fig.1: esempio di circuito elettrico
Leggi di Kirchhoff
I circuiti elettrici in corrente continua con un solo generatore e con serie e parallelo di resistori possono essere risolti riducendo in modo sistematico i blocchi in serie e in parallelo ai relativi resistori equivalenti. La procedura di riduzione non è attuabile nei circuiti in cui sono presenti più generatori o reti complesse di resistori. In questi casi si utilizza un procedimento analitico che consiste nell’impostare e risolvere un sistema lineare con tante equazioni quante sono le correnti incognite.
Queste equazioni si ottengono analizzando porzioni di circuito mediante l’applicazione di due princìpi, noti come leggi di Kirchhoff, dal nome del tedesco Gustav Kirchhoff (1824-1887).
Prima legge di Kirchhoff o legge dei nodi
Sia dato un circuito elettrico ed un suo nodo N che collega un certo numero di rami.
Per ogni ramo avremo una corrente elettrica che si dirà entrante se la freccia va verso il nodo N, uscente altrimenti.
Nell'immagine vi sono 5 rami connessi ad un unico nodo: 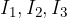 sono le correnti entranti mentre
sono le correnti entranti mentre 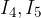 quelle uscenti.
quelle uscenti.
Premesso ciò, la prima legge di Kirchhoff o legge dei nodi si può esprimere nella forma seguente.
La somma aritmetica delle correnti entranti in un nodo è sempre uguale alla somma aritmetica delle correnti uscenti dal nodo
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Seconda legge di Kirchhoff o legge delle maglie
Supponiamo di muoverci all’interno di un circuito come quello di fig.1: il potenziale varia ogni volta che si attraversa un generatore o un resistore, aumentando o diminuendo a seconda del verso di percorrenza.
Occorre quindi uniformare il segno della variazione di potenziale attraverso l'introduzione di una convenzione dei segni.
Quando attraversiamo un generatore ideale:
dal - al + il potenziale sale di un valore pari alla forza elettromotrice del generatore (fem), 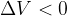 ;
;
dal + al - il potenziale scende di un valore pari alla fem, 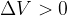 .
.
Quando attraversiamo un resistore con resistenza R:
nel verso della corrente, il potenziale scende di un valore pari a 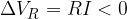 ;
;
nel verso opposto alla corrente, il potenziale sale di un valore pari a 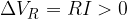 .
.
Consideriamo le variazioni di potenziale in una maglia, cioè in un tratto chiuso di circuito. Se si percorre l’intera maglia, si torna al punto di partenza, pertanto la somma delle salite di potenziale deve essere uguale ma di segno opposto a quello delle discese. Questo fatto è espresso dalla seconda legge di Kirchhoff o legge delle maglie.
La somma algebrica delle differenze di potenziale che si incontrano lungo una maglia è uguale a zero.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »




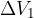 ,
, 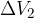 ,
, 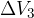 mentre rimangono incognite le coppie
mentre rimangono incognite le coppie 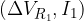 ,
, 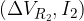 e
e 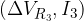 per ogni resistore.
per ogni resistore.
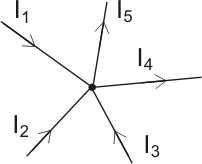
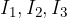 sono le correnti entranti mentre
sono le correnti entranti mentre 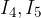 quelle uscenti.
quelle uscenti.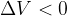 ;
;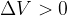 .
.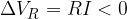 ;
;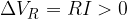 .
.


