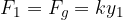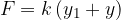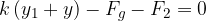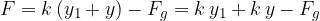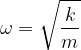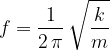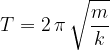Le molle fanno parte della vita quotidiana come parti di altri oggetti più o meno complicati (penne, giocattoli, meccanismi di vario genere, orologi...).

La molla permette il funzionamento delle comuni penne a sfera
Quale caratteristica della molla viene sfruttata?
La caratteristica principale delle molle è la sua capacità di allungarsi in modo elastico, cioè si allunga se viene applicata una forza e torna nella sua posizione di partenza una volta che la forza cessa.
Come sono fatte le molle?
Le molle elicoidali sono costituite da un cavo di acciaio, di solito a sezione circolare, (o di altro materiale a secondo dell'uso che se ne fa) avvolto intorno a un'ideale superficie cilindrica.
Immaginiamo di collegare una massa a una molla elicoidale: otteniamo un oscillatore armonico. Vediamo in dettaglio quali sono le caratteristiche di questo modello.
Nell'istante iniziale dell'osservazione la massa collegata alla molla è nella sua posizione di equilibrio, spostando la massa il sistema inizierà a oscillare intorno alla sua posizione di equilibrio.
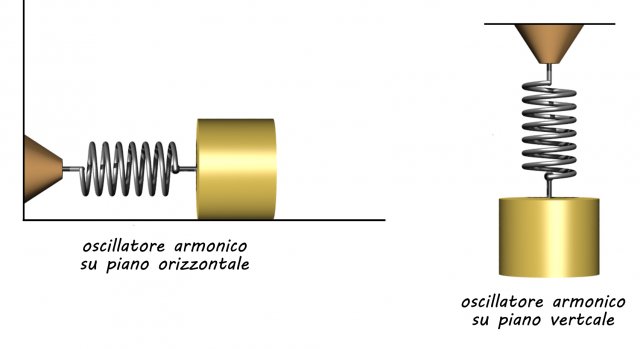
Ora analizzeremo due casi principali:
l'oscillatore è appoggiato su una superficie orizzontale
l'oscillatore è in posizione verticale
Superficie orizzontale
Consideriamo una massa m appoggiata su una superficie orizzontale (con un certo coefficiente d'attrito) e collegata a una molla elicoidale. In questo caso la forza di gravità dovuta alla massa m, agendo in direzione perpendicolare al movimento, non fa lavoro e quindi non influenza l'oscillazione.
Nella posizione di equilibrio, la forza della molla è uguale a zero. Nel momento in cui la massa si sposta dalla posizione di equilibrio nascono delle forze di richiamo per riportare la massa nella posizione di equilibrio. Durante le oscillazioni quindi abbiamo un continuo succedersi di conversioni tra energia cinetica e potenziale.
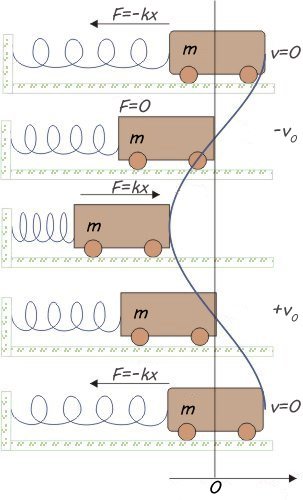
molla elicoidale in orizzontale
Comprimiamo la molla con una forza pari a:
Il termine a è un'accelerazione, in questo caso possiamo utilizzare la forma che definisce l'accelerazione nelle oscillazioni armoniche, cioè:
La molla compressa risponde con una forza che agisce nella direzione opposta.
Eguagliamo le due equazioni
Superficie verticale
Osserviamo ora il caso dell'oscillatore armonico in posizione verticale. In questo caso la forza di gravità, agendo nella direzione dello spostamento, fa lavoro e influenzerà le oscillazioni. Cerchiamo di capire se anche la frequenza delle oscillazioni verrà influenzata.
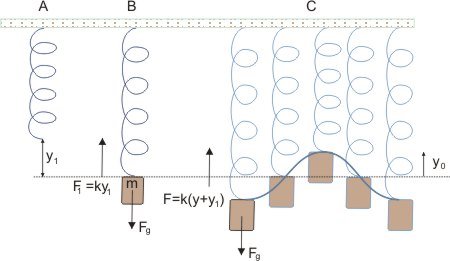
Molla fissata in verticale
In B viene agganciata una massa e la molla si allunga di 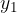 . L'allungamento è dovuto alla forza di gravità
. L'allungamento è dovuto alla forza di gravità 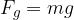 esercitata dalla massa
esercitata dalla massa
Nella nuova posizione di equilibrio la forza della molla è: 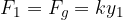
Se applichiamo una forza aggiuntiva, la molla si allungherà di un'ulteriore quantità y e la forza totale sarà data, secondo la Legge di Hooke, da:
Il sistema continuerà a oscillare finché non si giunge a una nuova posizione di equilibrio in cui:
In C la molla oscilla intorno a una nuova posizione di equilibrio in cui le forze in gioco sono:
Vediamo che il risultato non è influenzato dalla forza di gravità, quindi la gravità non ha alcuna influenza sulla frequenza di oscillazione.
Frequenza di oscillazione







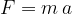
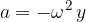
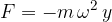
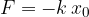

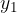 . L'allungamento è dovuto alla forza di gravità
. L'allungamento è dovuto alla forza di gravità 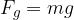 esercitata dalla massa
esercitata dalla massa