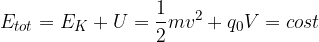Conservatività della forza di Coulomb
La forza di Coulomb  è una grandezza vettoriale alla base dei fenomeni elettrici.
è una grandezza vettoriale alla base dei fenomeni elettrici.
Abbiamo visto parlando di Forza di Coulomb che alla forza di Coulomb è sempre possibile associare un campo elettrico  .
.
La forza di Coulomb, in generale, può agire sulle cariche elettriche spostandole da un punto iniziale dello spazio considerato ad un determinato punto finale. Durante questo processo la forza compie del lavoro elettrico e il campo elettrico relativo associato alla forza prende il nome di campo elettromotore.
La forza di Coulomb, inoltre, è una forza conservativa in quanto gode delle seguenti proprietà (si ripassino i concetti di lavoro, conservatività di una forza ed energia potenziale trattati nel capitolo relativo alla Dinamica).
Il lavoro compiuto dalla forza di Coulomb su una carica che si sposta da un punto A a un punto B non dipende dalla traiettoria percorsa ma solo dalla posizione di A e B, quindi per ogni coppia di punti A e B è possibile definire univocamente il lavoro necessario alla forza per spostare una determinata carica dal punto A al punto B e lo indichiamo con 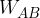 .
.
Il lavoro compiuto dalla forza di Coulomb su una carica che si sposta lungo un percorso chiuso è nullo 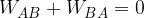 (vedi figura).
(vedi figura).
Ad ogni punto dello spazio in cui agisca la forza di Coulomb è associato un potenziale elettrostatico (V).
Ad ogni carica elettrica sottoposta all'azione della forza di Coulomb è associata una energia potenziale elettrica (U) che dipende dal valore della carica e dal potenziale elettrostatico del punto considerato.
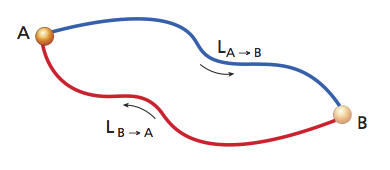
Lavoro della forza elettrica lungo un percorso chiuso
Differenza di potenziale elettrostatico
Abbiamo appena osservato che in presenza di un campo elettrostatico si manifesta l'azione della forza di Coulomb che risulta essere conservativa ed è pertanto associabile ad un potenziale elettrostatico V e quindi ad una energia potenziale U.
L’unità di misura del potenziale elettrico è joule/coulomb ed è chiamata Volt (V), in onore del fisico italiano Alessandro Volta (1745-1827):
In altre parole, la differenza di potenziale 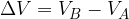 rappresenta l'energia necessaria per spostare un coulomb da un punto A ad un punto B sotto l'azione di un campo elettrostatico.
rappresenta l'energia necessaria per spostare un coulomb da un punto A ad un punto B sotto l'azione di un campo elettrostatico.
Ricordando che la carica di prova è per convenzione positiva, possiamo dare la seguente interpretazione al segno negativo della (1):
Potenziale elettrostatico
Abbiamo visto che la forza di Coulomb decresce con l'aumentare della distanza tra la carica generatrice del campo elettrostatico 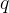 e la carica elettrica di prova
e la carica elettrica di prova 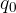 .
.
Dal momento che questa interazione è esprimibile come lavoro della forza, è lecito supporre che a distanza sufficientemente grande (o infinita) tale interazione sia nulla in modo tale da poter scrivere
Di conseguenza, se come punto di arrivo consideriamo un punto a distanza infinita (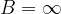 ), possiamo scrivere
), possiamo scrivere
e dalla (1) deduciamo che
Tale espressione fornisce una definizione operativa di potenziale elettrostatico.
Il potenziale  esprime il lavoro
esprime il lavoro  necessario per portare 1 C dal punto A del campo elettrostatico ad un punto posto a distanza infinita di potenziale nullo.
necessario per portare 1 C dal punto A del campo elettrostatico ad un punto posto a distanza infinita di potenziale nullo.
Il potenziale, oltre che alla distanza, è legato all'intensità della forza di Columb presente in quel punto e di conseguenza anche all'intensità del campo elettrostatico generato 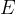 .
.
Poichè 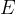 dipende dal valore della carica generatrice così anche
dipende dal valore della carica generatrice così anche 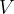 dipenderà da essa.
dipenderà da essa.
In ultimo, l'intensità del campo 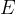 e
e 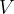 dipendono in ogni caso dalla materia (vuoto, aria, solido, etc.) in cui si sta osservando il fenomeno. Per semplicità d'ora in avanti considereremo le cariche in gioco immerse nel vuoto.
dipendono in ogni caso dalla materia (vuoto, aria, solido, etc.) in cui si sta osservando il fenomeno. Per semplicità d'ora in avanti considereremo le cariche in gioco immerse nel vuoto.
A questo punto siamo pronti per dare una espressione alternativa al potenziale elettrostatico.
dove 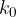 è la costante di Coulomb nel vuoto che vale
è la costante di Coulomb nel vuoto che vale
Ricordiamo che 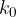 è legata alla costante dielettrica del vuoto
è legata alla costante dielettrica del vuoto 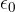 dalla
dalla
Energia potenziale elettrostatica
Nel paragrafo precedente abbiamo visto che il potenziale elettrostatico 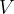 si può interpretare come energia per unità di carica in un certo punto del campo elettrostatico necessaria alla forza del campo per portare 1 Coulomb a distanza infinita dalla carica generatrice.
si può interpretare come energia per unità di carica in un certo punto del campo elettrostatico necessaria alla forza del campo per portare 1 Coulomb a distanza infinita dalla carica generatrice.
Si definisce energia potenziale elettrostatica di una carica 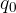 posta in un punto del campo la quantità
posta in un punto del campo la quantità
L'unità di misura è il Joule (J) dal fisico britannico James Prescott Joule (1818-1889): un Joule rappresenta la quantità di energia necessaria per spostare un Coulomb da un punto di potenziale di un Volt ad un punto di potenziale nullo.
Considerati due punti A e B del campo possiamo scrivere
e dalla (1) segue la relazione tra energia potenziale e lavoro
mentre sostituendo la (2) nella (3) abbiamo un'espressione alternativa dell'energia potenziale
Moto di una carica, conservazione dell'energia
Lo studio del moto di una carica immersa in un campo elettrico può essere effettuato tramite il principio di conservazione dell'energia totale in quanto il moto avviene in presenza di forze conservative.
D'altra parte il lavoro 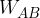 necessario per lo spostamento abbiamo visto essere legato al potenziale elettrostatico dalla (4)
necessario per lo spostamento abbiamo visto essere legato al potenziale elettrostatico dalla (4)
Combinando quest'ultima relazione con la (5) otteniamo
che esprime la conservazione dell'energia totale:
Durante il moto della particella l'energia totale data dalla somma dell'energia cinetica (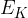 ) e dell'energia potenziale (
) e dell'energia potenziale (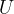 ) rimane costante
) rimane costante




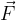 è una grandezza vettoriale alla base dei fenomeni elettrici.
è una grandezza vettoriale alla base dei fenomeni elettrici.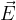 .
.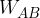 .
.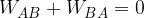 (vedi figura).
(vedi figura).
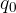 immersa in un campo elettrostatico
immersa in un campo elettrostatico 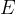 : per spostare la carica da un punto A ad un punto B dello spazio la forza di Coulomb dovrebbe compiere un certo lavoro chiamato
: per spostare la carica da un punto A ad un punto B dello spazio la forza di Coulomb dovrebbe compiere un certo lavoro chiamato 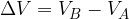 l'opposto del rapporto tra il lavoro
l'opposto del rapporto tra il lavoro 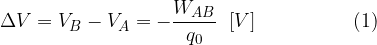
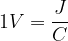
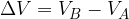 rappresenta l'energia necessaria per spostare un coulomb da un punto A ad un punto B sotto l'azione di un campo elettrostatico.
rappresenta l'energia necessaria per spostare un coulomb da un punto A ad un punto B sotto l'azione di un campo elettrostatico.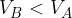 allora
allora 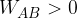 : la carica di prova si sposta spontaneamente dal punto A al punto B per effetto della forza di Coulomb;
: la carica di prova si sposta spontaneamente dal punto A al punto B per effetto della forza di Coulomb;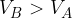 allora
allora 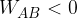 : la carica deve subire il lavoro di una forza esterna ed opposta alla forza di Coulomb per spostarsi da A a B.
: la carica deve subire il lavoro di una forza esterna ed opposta alla forza di Coulomb per spostarsi da A a B.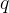 e la carica elettrica di prova
e la carica elettrica di prova 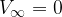
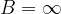 ), possiamo scrivere
), possiamo scrivere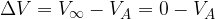
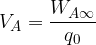
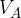 esprime il lavoro
esprime il lavoro 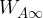 necessario per portare 1 C dal punto A del campo elettrostatico ad un punto posto a distanza infinita di potenziale nullo.
necessario per portare 1 C dal punto A del campo elettrostatico ad un punto posto a distanza infinita di potenziale nullo.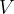 dipenderà da essa.
dipenderà da essa.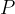 a distanza
a distanza  da una carica
da una carica 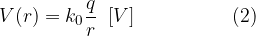
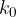 è la costante di Coulomb nel vuoto che vale
è la costante di Coulomb nel vuoto che vale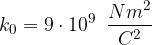
 dalla
dalla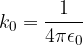
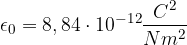
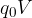 Coulomb per Volt: questa quantità prende il nome di energia potenziale elettrostatica e si denota con la lettera
Coulomb per Volt: questa quantità prende il nome di energia potenziale elettrostatica e si denota con la lettera 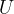 .
.
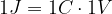
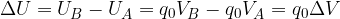

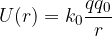
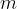 passa dalla posizione A in cui possiede una certa velocità
passa dalla posizione A in cui possiede una certa velocità 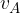 alla posizione B in cui possiede una velocità
alla posizione B in cui possiede una velocità 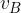 la sua energia cinetica cambia in accordo con il teorema dell'energia:
la sua energia cinetica cambia in accordo con il teorema dell'energia: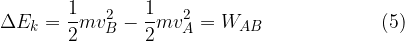
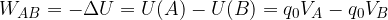
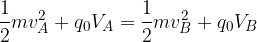
 ) e dell'energia potenziale (
) e dell'energia potenziale (