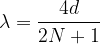Diffusione del suono
Nel capitolo Le Onde e il suono abbiamo visto che il suono è un susseguirsi di compressioni e di rarefazioni in un fluido (liquido o gas) e può essere rappresentato come delle onde con una certa lunghezza d'onda, e un preciso fronte d'onda (che è quella superficie che indica dove si trova la compressione). Naturalmente la distanza tra due fronti d'onda è pari alla lunghezza d'onda.
Se la sorgente è piana si generano onde piane; se la sorgente è puntiforme si generano onde sferiche.
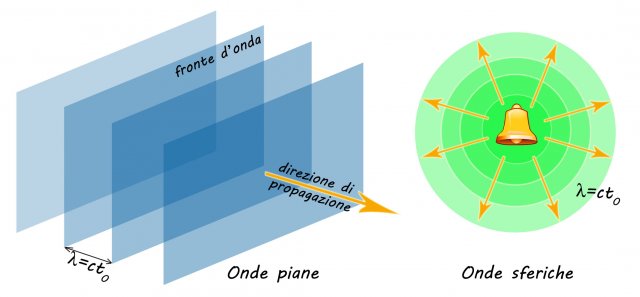
Onde piane e onde sferiche
Propagazione delle onde sonore in presenza di ostacoli
Vi sono diversi fenomeni legati alla propagazione di un’onda in presenza di ostacoli. Sono classificati come segue:
Il fenomeno della diffusione non è nient’altro che una combinazione di rifrazione e diffrazione.
Un'onda che incide su una superficie che separa due mezzi diversi viene parzialmente riflessa nel mezzo da cui proviene e parzialmente trasmessa (rifratta) nel nuovo mezzo.
Riflessione delle onde sonore
Quando un'onda sonora incontra un ostacolo può accadere che l'onda lo superi, oppure che venga riflessa o assorbita.
Come per le onde luminose anche per le onde sonore vale la legge di riflessione secondo la quale l'angolo di riflessione, rispetto alla normale alla superficie riflettente, è uguale all'angolo di incidenza dell'onda.
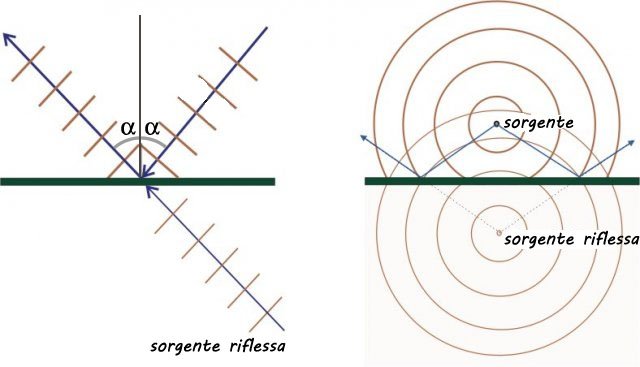
Riflessione di un'onda piana e di un'onda sferica
Rifrazione delle onde sonore
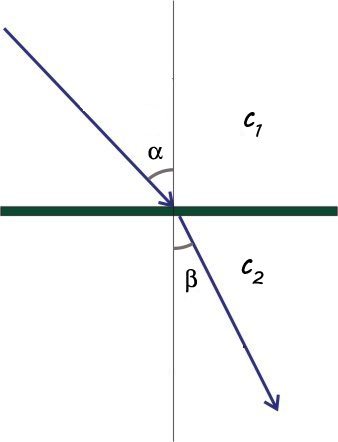
Anche le onde sonore sono soggette alla rifrazione. Questo fenomeno si verifica quando le onde attraversano aree nelle quali si propagano con velocità diverse, e perciò deviano la loro direzione.
Quindi si ha rifrazione al passaggio del suono tra mezzi diversi.
Si ha che il seno dell'angolo di incidenza e dell'angolo di rifrazione sono nella stessa proporzione della velocità nei due mezzi:
Il principio di sovrapposizione
Quando più persone parlano insieme succede che in uno stesso punto vengano rilevate più onde sonore. Cosa succede quando due o più onde si incontrano? Vediamo cosa succede con l'aiuto di una figura in cui sono rappresentati due impulsi:
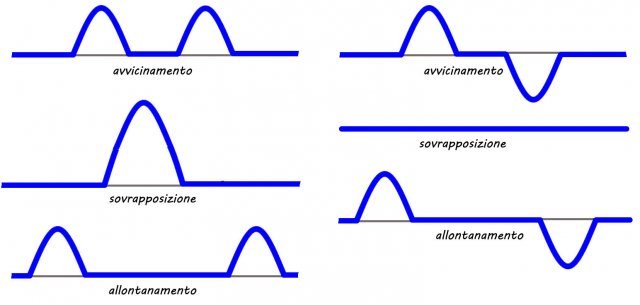
Sovrapposizione - interferenza costruttiva e distruttiva
Nella parte a sinistra i due impulsi sono entrambi rappresentati da spostamenti verso l'alto, e nel momento i cui si avvicinano e si sovrappongono i due impulsi si "sommano".
Analogamente, nella parte a destra della figura, i due impulsi sono rappresentati da spostamenti verso e l'alto e verso il basso, perciò quando si avvicinano e si sovrappongono la somma dei due impulsi è nulla. Questo fenomeno è descritto nel Principio di sovrapposizione.
Principio di sovrapposizione
Quando due o più onde sono presenti contemporaneamente in uno stesso punto, la perturbazione in quel punto è la somma delle perturbazioni prodotte dalle singole onde.
Interferenza
Il fenomeno dell'interferenza è strettamente legato al Principio di sovrapposizione e riguarda tutti i tipi di onde, non solo le onde sonore. Abbiamo visto che quando due o più onde interferiscono in un punto dello spazio accade che l'ampiezza dell'onda risultante può essere nulla o data dalla somma delle singole.
L'interferenza è costruttiva se l'intensità risultante è maggiore rispetto a quella di ogni singola intensità originaria, è distruttiva in caso contrario.
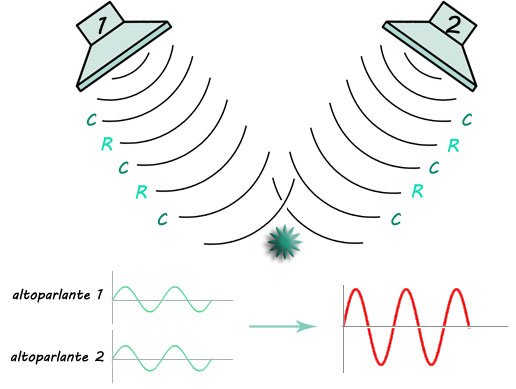
Immaginiamo di essere in un punto P di una stanza equidistante da due altoparlanti che trasmettono in fase (cioè iniziano a funzionare nello stesso istante) delle onde sonore di uguale lunghezza d'onda e frequenza.
In queste condizioni si ha la sovrapposizione delle compressioni C e delle rarefazioni R delle due onde.
Quindi, per il principio di sovrapposizione, nel punto P avremo che l'onda risultante sarà la somma delle due singole e perciò il suono che sentiremo sarà più forte di quello di un singolo altoparlante.
Se le compressioni si sovrappongono alle compressioni e le rarefazioni si sovrappongono alle rarefazioni, si dice che sono in fase e creano un'interferenza costruttiva.
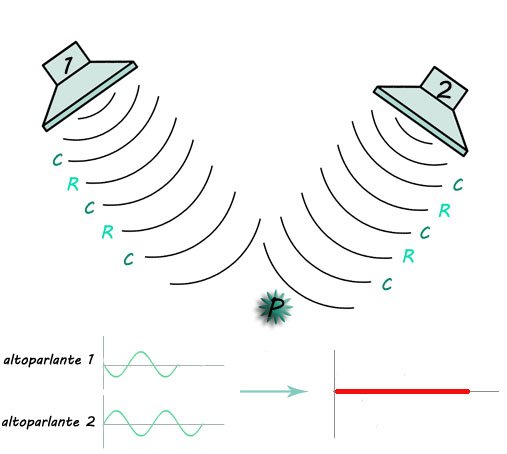
Se allontaniamo l'altoparlante di sinistra di mezza lunghezza d'onda, avremo che le compressioni delle due onde non si sovrappongono più, anzi che la compressione di una si sovrappone alla compressione dell'altra.
Quindi, per il principio di sovrapposizione, l’ampiezza dell’onda che risulta dalla combinazione di queste due onde è nulla perché le rarefazioni prodotte da un’onda compensano le compressioni dell'altra. Nel punto P non si sente alcun suono.
Se le compressioni di un'onda si sovrappongono alle rarefazioni dell'altra, si dice che sono in opposizione di fase e che creano un'interferenza distruttiva.
Nei punti in cui non si ha né interferenza costruttiva né interferenza distruttiva le due onde si combinano dando luogo a suoni di intensità un po’ maggiore o un po’ minore del suono emesso da ciascun altoparlante.
Vediamo come presentare l'interferenza in termini matematici con le funzioni d'onda.
due onde, sfasate di 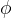 , che viaggiano nella stessa direzione, con la stessa velocità, la stessa frequenza e la stessa ampiezza.
, che viaggiano nella stessa direzione, con la stessa velocità, la stessa frequenza e la stessa ampiezza.
L'onda risultante dall'interferenza delle due è:
sfruttando le formule di prostaferesi:
Questa funzione d'onda rappresenta ancora un'onda che si propaga verso destra e sfasata di 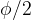 rispetto alle due onde. L'ampiezza dell'onda A' ora però è data da:
rispetto alle due onde. L'ampiezza dell'onda A' ora però è data da:
e notiamo che dipende solo dalla differenza di fase 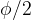 .
.
se 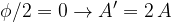 L'ampiezza risultante è il doppio dell'ampiezza di ciascuna onda, si ha interferenza costruttiva.
L'ampiezza risultante è il doppio dell'ampiezza di ciascuna onda, si ha interferenza costruttiva.
se 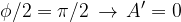 L'ampiezza risultante è nulla, si ha interferenza distruttiva.
L'ampiezza risultante è nulla, si ha interferenza distruttiva.
Onde stazionarie
Supponiamo ora di avere due onde di uguale ampiezza che viaggiano in direzioni opposte:
In seguito all'interferenza avremo:
Questa funzione d'onda non rappresenta un'onda che si propaga perché i termini spaziale e temporale sono separati, perciò l'onda è detta onda stazionaria. Le onde stazionarie sono chiamate così perché sembrano non muoversi.
In questo caso l'ampiezza è rappresentata dal termine:
quando il valore del coseno è nullo, l'ampiezza è nulla. Tali punti vengono chiamati nodi:
quando il valore del coseno è uno, si hanno gli antinodi, unti cioè dove l'ampiezza è massima:
Riflessione dell'onda sonora in una canna chiusa
Vediamo cosa succede a un'onda sonora quando incontra nel suo diffondersi nell'aria una parete o l'estremità di una canna chiusa.
Appena la zona di compressione dell'onda "sbatte" contro la parete, non potendo più oscillare le particelle d'aria rimbalzano contro la parete producendo un abbassamento della pressione.
Si dice allora che la pressione presenta un ventre e viene riflessa senza inversione di fase.
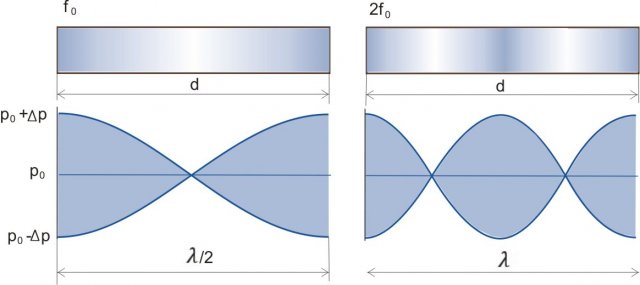
Canna chiusa su entrambe le estremità: frequenza fondamentale e prima armonica
La lunghezza della canna e la lunghezza d'onda sono legate dalla seguente relazione:
in cui N è un numero naturale.
Ricaviamo anche un'espressione per la frequenza:
Se N = 1 ricaviamo la frequenza fondamentale, se N = 2 troviamo la prima armonica.
Riflessione dell'onda sonora in una canna aperta
Le frequenze normali di onde stazionarie in una canna con un’estremità chiusa e una aperta sono spaziate di 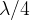 , il motivo risiede nel fatto che all'estremità aperta la pressione deve essere necessariamente pari alla pressione atmosferica.
, il motivo risiede nel fatto che all'estremità aperta la pressione deve essere necessariamente pari alla pressione atmosferica.
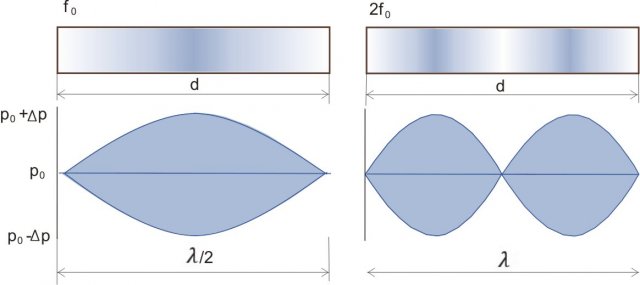
Canna aperta alle estremità: frequenza fondamentale e prima armonica
La lunghezza d'onda e la lunghezza della canna sono legate tramite la relazione:
dove N è un numero naturale. La lunghezza d'onda quindi è:
Ricaviamo anche la frequenza:
Se N = 1, avremo la frequenza fondamentale, se N = 2 troviamo la prima armonica.
Canna semi-aperta
Vediamo ora il caso di una canna semi-aperta.
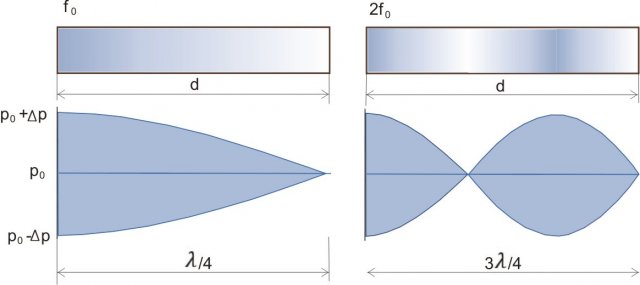
Canna semiaperta: frequenza fondamentale e prima armonica
La lunghezza d'onda e la lunghezza della canna sono legate tramite la relazione:
Ricaviamo 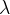 :
:
Se N = 0, troviamo la frequenza fondamentale, se N = 1 troviamo la prima armonica.






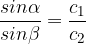


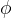 , che viaggiano nella stessa direzione, con la stessa velocità, la stessa frequenza e la stessa ampiezza.
, che viaggiano nella stessa direzione, con la stessa velocità, la stessa frequenza e la stessa ampiezza.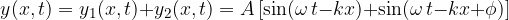
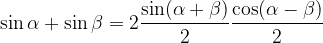
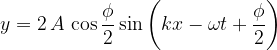
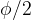 rispetto alle due onde. L'ampiezza dell'onda A' ora però è data da:
rispetto alle due onde. L'ampiezza dell'onda A' ora però è data da: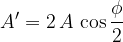
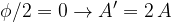 L'ampiezza risultante è il doppio dell'ampiezza di ciascuna onda, si ha interferenza costruttiva.
L'ampiezza risultante è il doppio dell'ampiezza di ciascuna onda, si ha interferenza costruttiva.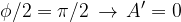 L'ampiezza risultante è nulla, si ha interferenza distruttiva.
L'ampiezza risultante è nulla, si ha interferenza distruttiva.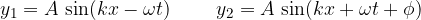
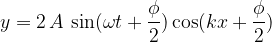
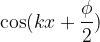
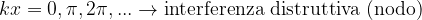
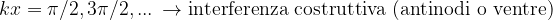

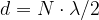
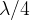 , il motivo risiede nel fatto che all'estremità aperta la pressione deve essere necessariamente pari alla pressione atmosferica.
, il motivo risiede nel fatto che all'estremità aperta la pressione deve essere necessariamente pari alla pressione atmosferica.
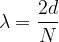

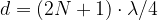
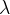 :
: