Spesso nella vita quotidiana avvengono fenomeni (lancio di un dado regolare, gioco del lotto, ecc.) il cui risultato non è noto a priori - chiamati esperimenti aleatori -: ogni risultato può possedere un "grado di fiducia" attribuito più o meno intuitivamente (esperienza personale, ripetizione dell'esperimento un numero grande di volte, ecc.).
Tale "grado di fiducia" è chiamato probabilità.
In questo capitolo cercheremo di introdurre strumenti elementari per studiarla matematicamente nei casi più semplici.
Una prima definizione di probabilità è quella più intuitiva dovuta al fatto che molti esperimenti aleatori non siano truccati, ovvero che non c'è preferenza in un risultato piuttosto che un altro.
La probabilità di un evento è il rapporto tra il numero dei casi favorevoli all'evento e il numero dei casi possibili.
Se indichiamo con 
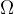l'insieme dei casi possibili, A un evento e 
la quantità di elementi di un insieme allora possiamo esplicitare la definizione di probabilità di un evento.
La probabilità di un evento A è il rapporto:
dove è l'insieme dei casi possibili.
Segue immediatamente:
Vediamo un esempio.
Un'altro modo per definire la probabilità è quella di affidarla a posteriori tramite rilevazione statistica: un esperimento aleatorio può essere ripetuto un numero arbitrario di volte nelle medesime condizioni.
In tal caso la probabilità di un evento diventa la frequenza relativa con cui esso viene rilevato.
La probabilità di un evento A è il rapporto:
dove 
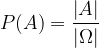
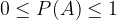
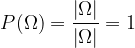
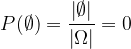
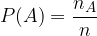
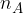è la frequenza assoluta dell'evento A e n è il numero di rilevazioni (arbitrariamente grandi).
Vediamo un esempio.
Le definizioni precedenti che abbiamo proposto hanno dei limiti:
Non tutti i risultati di un esperimento aleatorio sono equiprobabili.
Un esperimento aleatorio potrebbe non essere replicabile molte volte nelle medesime condizioni.
Per aggirare questi problemi possiamo incaricarci di definire la probabilità di un evento come "scommessa":
La probabilità di un evento è il prezzo che un individuo ritiene equo pagare per ricevere 1 se l'evento si verifica, 0 se l'evento non si verifica. Le probabilità degli eventi devono essere attribuite in modo tale che non sia possibile ottenere una vincita o una perdita certa.
Vediamo un esempio.
In questo capitolo si fanno riferimento a nozioni di insiemistica e sulle serie numeriche.
La definizione soggettiva non permette di avere un criterio oggettivo o logico per poter attribuire delle probabilità in maniera univoca: molti di noi sarebbero ben disposti a scommettere 1 € per vincerne 1000 €, ma ben pochi sarebbero disposti a scommetterne 1000000 € per vincerne 1000000000 €.
Per superare tale difficoltà non diamo una definizione operativa di probabilità (cos'è), ma stabiliamo regole ragionevoli che una probabilità deve rispettare:
Sia un insieme finito oppure numerabile, 
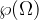il suo insieme delle parti.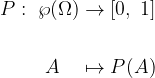
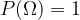
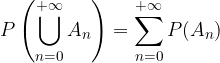Una probabilità è una funzione:
tale che:
dove gli insiemi 
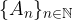sono a 2 a 2 disgiunti (
)
L'insieme si chiama spazio campionario mentre la proprietà 2 è chiamata 
-additività.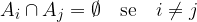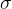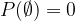
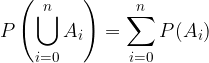La coppia ordinata (, P) si chiama spazio di probabilità discreto.
Indipendentemente dalla definizione di probabilità assunta essa rispetta gode di alcune proprietà.
dove gli insiemi 
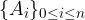sono a 2 a 2 disgiunti ().
La proprietà 2 è chiamata Additività finita.
Vediamo un esempio:
