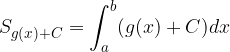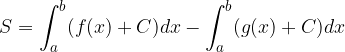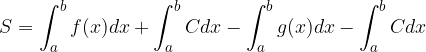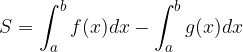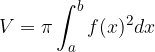Un integrale definito si indica con la scrittura
dove 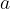 è detto estremo inferiore e
è detto estremo inferiore e 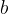 è detto estremo superiore dell'integrale.
è detto estremo superiore dell'integrale.
Il calcolo di un integrale definito serve a determinare l'area di una superficie piana delimitata da contorni curvilinei. In particolare, se consideriamo la scrittura precedente, l'integrale definito servirà a calcolare l'area della superficie piana compresa tra:
la curva descritta dalla funzione f(x), continua e non negativa
Definizione di integrale definito
Questo paragrafo è destinato agli studenti che desiderano approfondire la teoria che sta alla base del concetto di integrale definito. Gli studenti che sono interessati esclusivamente all'applicazione pratica finalizzata al calcolo delle aree possono tralasciarlo e passare ai paragrafi successivi.
Vogliamo calcolare l'area della superficie piana all'interno dell'intervallo 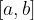 compresa tra la curva della funzione f(x) e dall'asse delle ascisse, così come rappresentata graficamente in precedenza.
compresa tra la curva della funzione f(x) e dall'asse delle ascisse, così come rappresentata graficamente in precedenza.
Dividiamo dunque l'intervallo 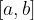 in tanti intervalli più piccoli:
in tanti intervalli più piccoli:
L'ampiezza degli intervalli è data da:
Dividiamo ulteriormente ogni intervallo, individuando all'interno di ciascuno di essi un punto di ascissa 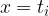 tale che:
tale che:
Disegniamo ora tanti rettangoli aventi come base l'ampiezza degli intervalli individuati 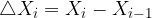 e per altezza i punti della funzione
e per altezza i punti della funzione 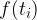 così come rappresentato nella figura seguente:
così come rappresentato nella figura seguente:
L'area di ciascuno di tali rettangoli sarà data dal prodotto:
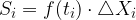 .
.
Se però consideriamo intervalli sempre più piccoli rispetto a quelli considerati, la somma delle aree dei rettangoli nell'intervallo 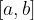 si avvicinerà sempre di più alla misura reale dell'area della superficie piana che stiamo cercando
si avvicinerà sempre di più alla misura reale dell'area della superficie piana che stiamo cercando
Quanto appena affermato equivale a calcolare il limite:
Tale limite è detto integrale definito.
Significato geometrico dell'integrale definito
Questo capitolo riguarda esclusivamente il significato geometrico degli integrali definiti. Esempi di calcolo integrale saranno trattati successivamente.
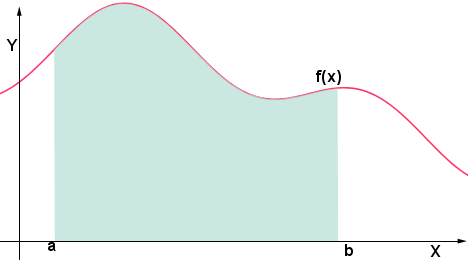
Il valore dell'integrale definito della funzione equivale all'area della superficie colorata.
Se S è l'area della superficie suddetta, avremo quindi:
Relazione tra integrale indefinito e definito di una funzione
La relazione esistente tra integrale indefinito e definito di una funzione è espressa dalla formula di Newton-Leibniz ovvero dal teorema fondamentale del calcolo integrale:
che possiamo anche rappresentare con la scrittura:
L'integrale definito di una funzione è uguale alla differenza dei valori assunti dai rispettivi integrali indefiniti della funzione rispettivamente nell'estremo superiore e inferiore dell'integrale stesso.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Proprietà degli integrali definiti
L'integrale della somma di due funzioni è uguale alla somma degli integrali delle singole funzioni:
Se 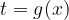 è una funzione derivabile nell'intervallo
è una funzione derivabile nell'intervallo 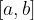 allora:
allora:
Posto 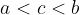 , allora avremo:
, allora avremo:
Posto 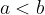 , invertire il verso dell'intervallo equivale a cambiare di segno l'integrale:
, invertire il verso dell'intervallo equivale a cambiare di segno l'integrale:
Se gli estremi dell'intervallo coincidono, allora l'integrale è zero:
L'integrale del prodotto di una costante per una funzione equivale al prodotto tra la costante e l'integrale della funzione:
Valore medio di una funzione
Il valore 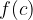 viene detto valore medio della funzione nell'intervallo considerato.
viene detto valore medio della funzione nell'intervallo considerato.
Il valore medio della funzione 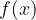 nell'intervallo
nell'intervallo 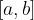 è:
è:
Applicazioni dell'integrale definito
Calcolo dell'area compresa tra una curva e l'asse delle ascisse

Il valore dell'integrale definito corrisponde all'area colorata.
Se indichiamo con S l'area della superficie suddetta, avremo:
In base a quanto affermato, dunque, l'area di una superficie delimitata da una funzione f(x) in un dato intervallo e dall'asse delle ascisse, corrisponde sempre al valore assoluto dell'integrale definito in quell'intervallo:
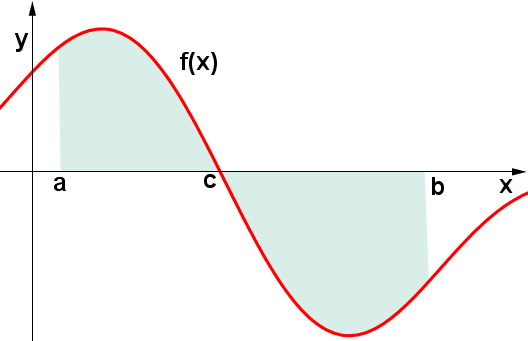
Vediamo un altro esempio e consideriamo una funzione 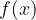 che, nell'intervallo
che, nell'intervallo 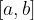 , sia continua e che assuma valori sia positivi che negativi:
, sia continua e che assuma valori sia positivi che negativi:
L'integrale definito 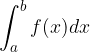 corrisponde alla differenza tra l'area della superficie delimitata dalla funzione al di sopra dell'asse delle ascisse e l'area della superficie delimitata dalla funzione al di sotto dell'asse delle ascisse. Poiché, però, come abbiamo visto, per l'area al di sotto dell'asse delle ascisse l'integrale restituisce un valore negativo, quanto appena detto equivale a sommare l'integrale della funzione nell'intervallo positivo e il valore assoluto della funzione nell'intervallo negativo:
corrisponde alla differenza tra l'area della superficie delimitata dalla funzione al di sopra dell'asse delle ascisse e l'area della superficie delimitata dalla funzione al di sotto dell'asse delle ascisse. Poiché, però, come abbiamo visto, per l'area al di sotto dell'asse delle ascisse l'integrale restituisce un valore negativo, quanto appena detto equivale a sommare l'integrale della funzione nell'intervallo positivo e il valore assoluto della funzione nell'intervallo negativo:
Calcolo dell'area compresa tra i grafici di due funzioni
Vediamo ora come calcolare l'area della superficie piana compresa tra due curve in un sistema di assi cartesiani, all'interno di un intervallo definito e al di sopra dell'asse delle ascisse.
Consideriamo le funzioni 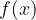 e
e 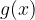 :
:
Vediamo più nel dettaglio quanto affermato.
Caso 1: f(x) e g(x) nell'intervallo [a,b] si trovano al di sopra dell'asse delle ascisse
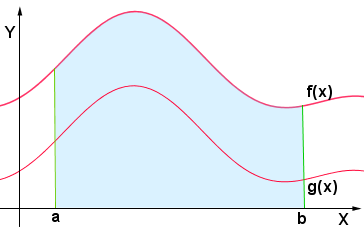
Calcoliamo per prima l'area della superficie delimitata dalla curva 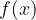 e l'asse delle ascisse:
e l'asse delle ascisse:
Sappiamo che nell'intervallo 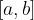 l'area di tale superficie corrisponde all'integrale definito:
l'area di tale superficie corrisponde all'integrale definito:
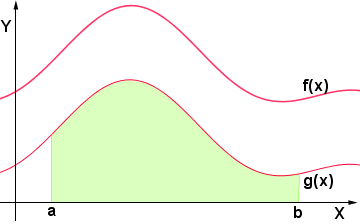
Analogamente, calcoliamo l'area della superficie piana compresa tra la curva 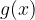 e l'asse delle ascisse:
e l'asse delle ascisse:
L'area di tale superficie è data da:
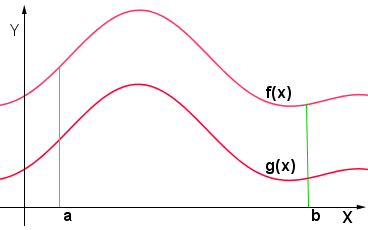
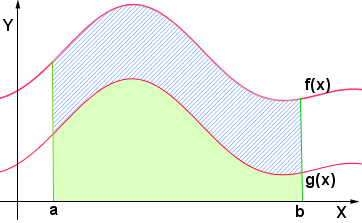
Stiamo però cercando l'area della superficie piana compresa tra le due curve:
Come si può vedere dalla figura, tale area corrisponde alla differenza delle aree:
Caso 2: f(x) e g(x) nell'intervallo [a,b] si trovano al di sotto dell'asse delle ascisse
Consideriamo le funzioni 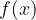 e
e 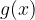 :
:
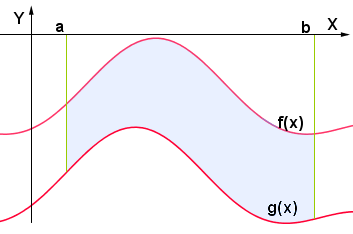
Pur considerando le nuove funzioni 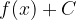 e
e 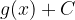 , l'area della superficie che desideravamo calcolare non cambia (resta uguale a quella originale). Possiamo quindi calcolare l'area della superficie tratteggiata nel seguente modo:
, l'area della superficie che desideravamo calcolare non cambia (resta uguale a quella originale). Possiamo quindi calcolare l'area della superficie tratteggiata nel seguente modo:
L'area della superficie delimitata dalla funzione 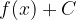 e l'asse delle ascisse è:
e l'asse delle ascisse è:
L'area della superficie delimitata dalla funzione 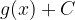 e l'asse delle ascisse è:
e l'asse delle ascisse è:
La differenza tra le due aree sarà data da:
Poiché sappiamo che l'integrale di una somma equivale alla somma degli integrali:
e che, come possiamo vedere, gli integrali della stessa costante si annullano tra loro, avremo che l'area della superficie desiderata è data da:
Volume dei solidi di rotazione
Se ruotiamo di 360° intorno all'asse delle ascisse la superficie piana compresa tra la funzione 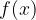 e l'asse delle ascisse stesso nell'intervallo
e l'asse delle ascisse stesso nell'intervallo 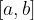 , otterremo un solido di rotazione.
, otterremo un solido di rotazione.
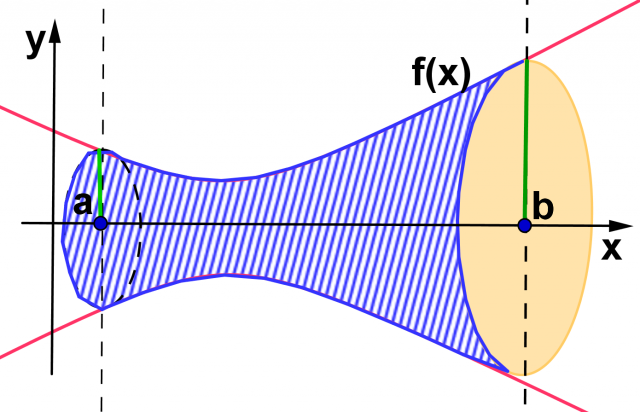
Curva della funzione 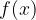 ruotata di 360° intorno all'asse x.
ruotata di 360° intorno all'asse x.
Il volume dei solidi ottenuti dalla rotazione di una funzione 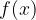 per 360° intorno all'asse delle ascisse è dato dall'integrale definito:
per 360° intorno all'asse delle ascisse è dato dall'integrale definito:





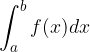
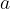 è detto estremo inferiore e
è detto estremo inferiore e 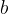 è detto estremo superiore dell'integrale.
è detto estremo superiore dell'integrale.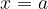 e
e 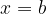
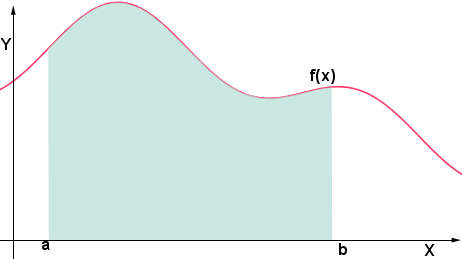
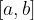 compresa tra la curva della funzione f(x) e dall'asse delle ascisse, così come rappresentata graficamente in precedenza.
compresa tra la curva della funzione f(x) e dall'asse delle ascisse, così come rappresentata graficamente in precedenza.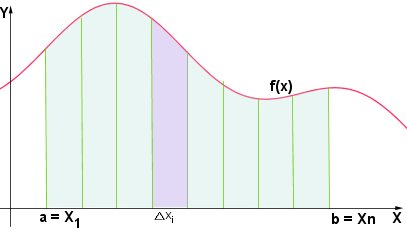
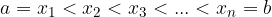
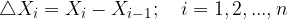
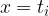 tale che:
tale che: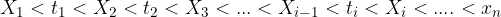
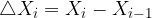 e per altezza i punti della funzione
e per altezza i punti della funzione 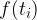 così come rappresentato nella figura seguente:
così come rappresentato nella figura seguente: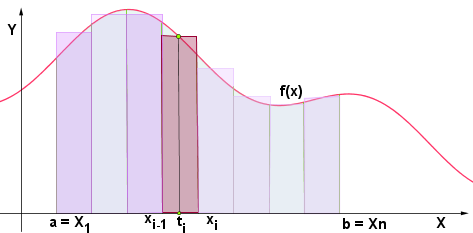
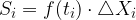 .
.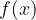 , dall'asse delle ascisse e dalle rette
, dall'asse delle ascisse e dalle rette 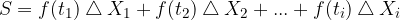
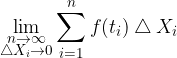
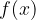 nell'intervallo
nell'intervallo 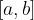 è dato dal limite
è dato dal limite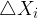 di tali intervalli tendente a
di tali intervalli tendente a 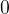 :
: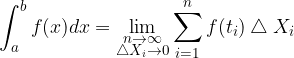
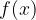 nell'intervallo
nell'intervallo 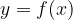 nell'intervallo
nell'intervallo 
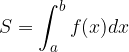
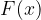 una qualunque sua primitiva, l'integrale indefinito di
una qualunque sua primitiva, l'integrale indefinito di 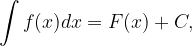
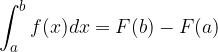
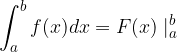
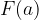 e sottrarlo dal valore che essa assume nell'estremo superiore
e sottrarlo dal valore che essa assume nell'estremo superiore 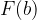 .
.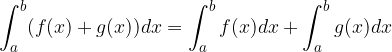
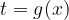 è una funzione derivabile nell'intervallo
è una funzione derivabile nell'intervallo 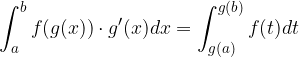
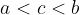 , allora avremo:
, allora avremo: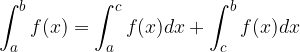
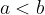 , invertire il verso dell'intervallo equivale a cambiare di segno l'integrale:
, invertire il verso dell'intervallo equivale a cambiare di segno l'integrale: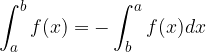
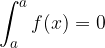
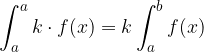
 interno all'intervallo, tale che:
interno all'intervallo, tale che: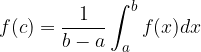
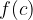 viene detto valore medio della funzione nell'intervallo considerato.
viene detto valore medio della funzione nell'intervallo considerato.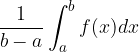
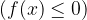 :
: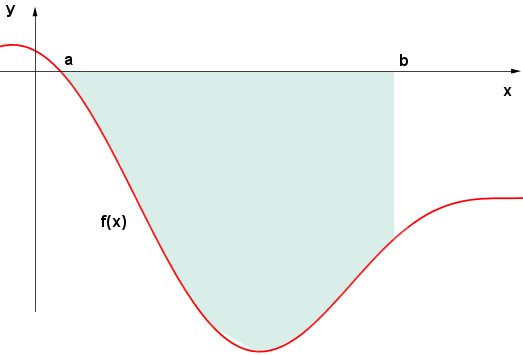
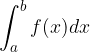 ha un valore negativo. Ma poiché non ha senso parlare di aree negative, dobbiamo considerare il valore assoluto ottenuto dall'integrale. In altre parole, l'area della superficie piana compresa tra la curva
ha un valore negativo. Ma poiché non ha senso parlare di aree negative, dobbiamo considerare il valore assoluto ottenuto dall'integrale. In altre parole, l'area della superficie piana compresa tra la curva 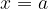 e
e 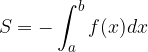
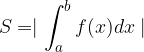
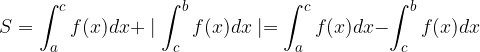
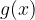 :
:
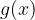 continue nell'intervallo
continue nell'intervallo 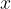 nel suddetto intervallo sia
nel suddetto intervallo sia 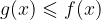 , sarà data da:
, sarà data da: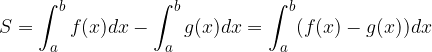

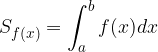
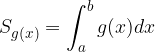
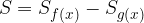
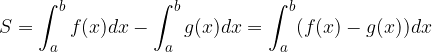
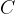 , sufficientemente grande, tale che le curve siano traslate oltre l'asse delle ascisse.
, sufficientemente grande, tale che le curve siano traslate oltre l'asse delle ascisse.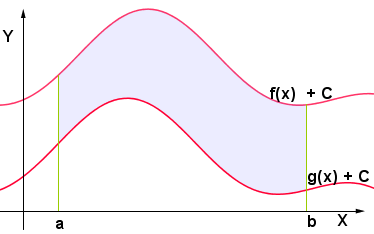
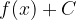 e
e 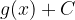 , l'area della superficie che desideravamo calcolare non cambia (resta uguale a quella originale). Possiamo quindi calcolare l'area della superficie tratteggiata nel seguente modo:
, l'area della superficie che desideravamo calcolare non cambia (resta uguale a quella originale). Possiamo quindi calcolare l'area della superficie tratteggiata nel seguente modo: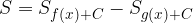
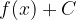 e l'asse delle ascisse è:
e l'asse delle ascisse è: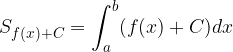
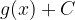 e l'asse delle ascisse è:
e l'asse delle ascisse è: