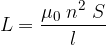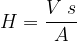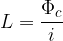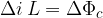Flusso magnetico
Abbiamo visto nel capitolo dedicato che il Campo magnetico è caratterizzato da linee di forza tangenti alle direzioni che vengono assunte dall'ago magnetico di prova nei diversi punti dello spazio ed orientate nel verso indicato dal polo nord dell'ago. Tali linee vengono comunemente chiamate linee di induzione magnetica.
L'insieme delle linee di induzione magnetica costituisce il flusso magnetico del campo e si indica con la lettera greca 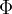 (leggasi "fi").
(leggasi "fi").
Quella parte delle linee di induzione che vengono effettivamente abbracciate in un dato momento da un circuito qualunque costituisce nel suo insieme il flusso concatenato con quel determinato circuito e si indica con 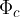 .
.
Legge di Faraday-Neumann dell'induzione elettromagnetica
Immaginiamo che un filo conduttore sia avvolto alle superfici di un magnete cilindrico: tale configurazione prende il nome di solenoide.
La legge di Faraday-Neumann afferma quanto segue.
Se n sono gli avvolgimenti del filo conduttore, la tensione indotta si può scrivere come
Se colleghiamo il filo conduttore ad un resistore R osserveremo il fluire, attraverso il circuito siffatto, di una corrente elettrica di intensità
La giustificazione del termine forza elettromotrice (indotta) per 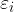 sta nel fatto che se si interrompe il circuito in un punto (annullando quindi la corrente) e si misura la differenza di potenziale ai capi del filo conduttore (ossia a vuoto) essa non sarà nulla ma pari proprio a
sta nel fatto che se si interrompe il circuito in un punto (annullando quindi la corrente) e si misura la differenza di potenziale ai capi del filo conduttore (ossia a vuoto) essa non sarà nulla ma pari proprio a 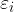 : la fem indotta si comporta quindi come la fem di un generatore ideale di tensione quando non passa corrente.
: la fem indotta si comporta quindi come la fem di un generatore ideale di tensione quando non passa corrente.
Il flusso magnetico può variare nel tempo attraverso gli avvolgimenti del conduttore per due motivi:
se varia nel tempo la superficie concatenata con le linee di forza del campo magnetico, ossia
se varia nel tempo il flusso del campo magnetico attraverso l'avvolgimento, cioè
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Unità di misura del flusso magnetico
Dagli esperimenti fatti sulla legge di Faraday-Neumann risulta che il numero di prodotto della tensione prodotta in un circuito per la durata della tensione prodotta dipende unicamente dalla variazione subita dal flusso concatenato con il circuito:
Grazie a queste considerazioni possiamo ora esprimere l'unità di misura del flusso magnetico come volt per secondo oppure, in onore al fisico tedesco Wilhelm Eduard Weber (1804-1891), come Weber (Wb)
Densità di flusso o vettore di induzione B
Dividendo il flusso magnetico 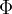 per la superficie
per la superficie 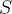 di un circuito che lo taglia, otteniamo il flusso per unità di superficie.
di un circuito che lo taglia, otteniamo il flusso per unità di superficie.
Il flusso riferito all'unità di superficie normale alle linee di induzione 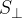 si definisce densità di flusso del campo e questa quantità viene semplicemente denominata induzione magnetica e designata con la lettera B.
si definisce densità di flusso del campo e questa quantità viene semplicemente denominata induzione magnetica e designata con la lettera B.
Per quanto detto possiamo scrivere un'espressione per il modulo del vettore induzione magnetica 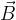 :
:
Se la superficie considerata 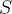 è perpendicolare alle linee di induzione del campo allora
è perpendicolare alle linee di induzione del campo allora
Se la superficie 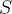 non è perpendicolare alle linee di induzione ma la sua normale forma un angolo
non è perpendicolare alle linee di induzione ma la sua normale forma un angolo 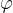 con esse dobbiamo introdurre allora un fattore in modo che sia unitario nel caso ideale di perpendicolarità:
con esse dobbiamo introdurre allora un fattore in modo che sia unitario nel caso ideale di perpendicolarità:
L'unità di misura dell'induzione magnetica è il Weber su metro quadrato e prende il nome di Tesla (T) dal nome del fisico croato attivo negli USA Nicola Tesla (1857-1943):
Alcune considerazioni sui casi limite che si possono incontrare al variare dell'angolo 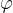 .
.
Autoinduzione
Consideriamo un filo conduttore avvolto a spirale (detto anche solenoide) in aria e percorso dalla corrente i. Per effetto del passaggio di corrente si genera un campo magnetico le cui linee di forza presentano l'andamento mostrato in figura.
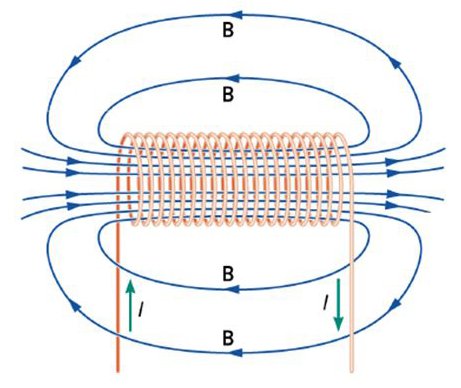
Linee di campo magnetico in un solenoide
Indichiamo con S la sezione del solenoide, con l la sua lunghezza e con n il numero di spire, ossia il numero di avvolgimenti su sé stesso del filo conduttore. Se la corrente varia nel tempo anche il flusso generato varia nel tempo producendo una forza elettromotrice indotta 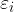 per la legge di Faraday-Neumann-Lenz: questo fenomeno prende il nome di autoinduzione.
per la legge di Faraday-Neumann-Lenz: questo fenomeno prende il nome di autoinduzione.
L'espressione della tensione indotta può essere derivata dall'espressione (3) vista precedentemente nel seguente modo.
Il primo fattore nella parte destra dell'equazione appena derivata dipende solo dalla geometria del solenoide e dal nucleo su cui esso è avvolto.
Si definisce induttanza (L) di un solenoide avvolto in aria (o vuoto) di lunghezza l sufficientemente grande, formato da n spire e di sezione S la quantità
L'unità di misura è l'Henry (H)
L'induttanza di un circuito può definirsi come il flusso che si concatena col circuito quando questo è percorso dall'unità di corrente. L'induttanza è perciò definita come
Se la corrente varia nel tempo, possiamo scrivere
ed applicando la legge di Faraday-Neumann arriviamo alla seguente conclusione:
Quando la corrente i che attraversa un solenoide di induttanza L varia nel tempo, si genera una fem autoindotta ai capi del solenoide di valore pari a
Un solenoide i cui parametri siano fissati possiederà quindi una determinata induttanza: tale componente fisico viene comunemente chiamato induttore.
Legge di Lenz
Qual è il significato del segno negativo della tensione indotta, nell'equazione (4) appena vista?
Tale segno è l'apporto del fisico Heinrich Friedrich Emil Lenz alla legge di Faraday-Neumann dell'autoinduzione e porta il nome di Legge di Lenz.
Il segno della tensione indotta è tale che la corrente circolante si opponga alla causa che l'ha generata, ossia alla variazione del flusso magnetico (in accordo con il terzo principio della dinamica o principio di azione e reazione).




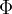 (leggasi "fi").
(leggasi "fi").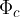 .
.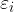 proporzionale al flusso concatenato
proporzionale al flusso concatenato 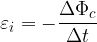
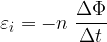
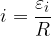
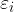 sta nel fatto che se si interrompe il circuito in un punto (annullando quindi la corrente) e si misura la differenza di potenziale ai capi del filo conduttore (ossia a vuoto) essa non sarà nulla ma pari proprio a
sta nel fatto che se si interrompe il circuito in un punto (annullando quindi la corrente) e si misura la differenza di potenziale ai capi del filo conduttore (ossia a vuoto) essa non sarà nulla ma pari proprio a 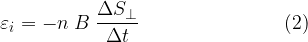
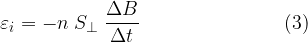
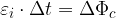
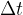 (tale quantità viene anche chiamata voltsecondo).
(tale quantità viene anche chiamata voltsecondo).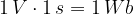
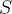 di un circuito che lo taglia, otteniamo il flusso per unità di superficie.
di un circuito che lo taglia, otteniamo il flusso per unità di superficie.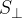 si definisce densità di flusso del campo e questa quantità viene semplicemente denominata induzione magnetica e designata con la lettera B.
si definisce densità di flusso del campo e questa quantità viene semplicemente denominata induzione magnetica e designata con la lettera B.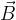 :
: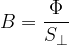
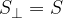
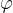 con esse dobbiamo introdurre allora un fattore in modo che sia unitario nel caso ideale di perpendicolarità:
con esse dobbiamo introdurre allora un fattore in modo che sia unitario nel caso ideale di perpendicolarità: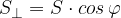
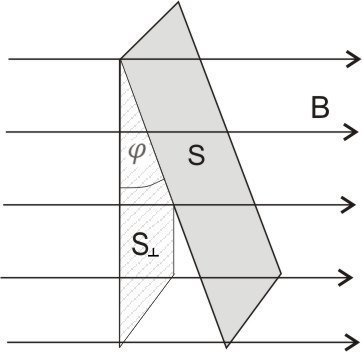
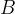 del campo magnetico di flusso
del campo magnetico di flusso 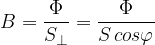
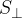 .
.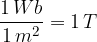
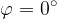 e quindi
e quindi 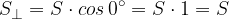 : il flusso magnetico
: il flusso magnetico 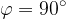 e quindi
e quindi 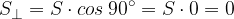 : il flusso magnetico
: il flusso magnetico 
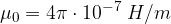 . La permeabilità assoluta di un mezzo generico si ottiene moltiplicando
. La permeabilità assoluta di un mezzo generico si ottiene moltiplicando 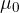 per un coefficiente relativo adimensionale
per un coefficiente relativo adimensionale 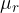 che dipende dal materiale
che dipende dal materiale 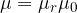 ).
).