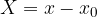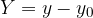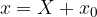In che modo si può identificare in maniera univoca (cioè senza possibilità di fraintendimenti) un punto?
Per identificare in maniera univoca un punto dobbiamo innanzitutto inserirlo in un sistema di riferimento, dopodiché assegnargli delle coordinate.
Ad esempio nella battaglia navale, un gioco in cui le navi occupano uno o più quadrati di una griglia, le posizioni delle navi sono identificate univocamente mediante una lettera ed un numero. Per "bombardare" un quadrato basta dare una coppia di coordinate, ad esempio A1.
Nei prossimi paragrafi ci occuperemo di punti che giacciono tutti su uno stesso piano.
Prendiamo due rette perpendicolari fra loro e assegniamo loro un'orientazione (ad esempio "in alto" o "in basso", "a sinistra" o "a destra"). In questo modo abbiamo stabilito un sistema di riferimento per il piano contenente le due rette.
Il loro punto di intersezione prende il nome di origine del sistema di riferimento, e le due rette si chiamano assi .
Fissiamo un'unità di misura su entrambi gli assi: sarà utile quando parleremo di distanze.
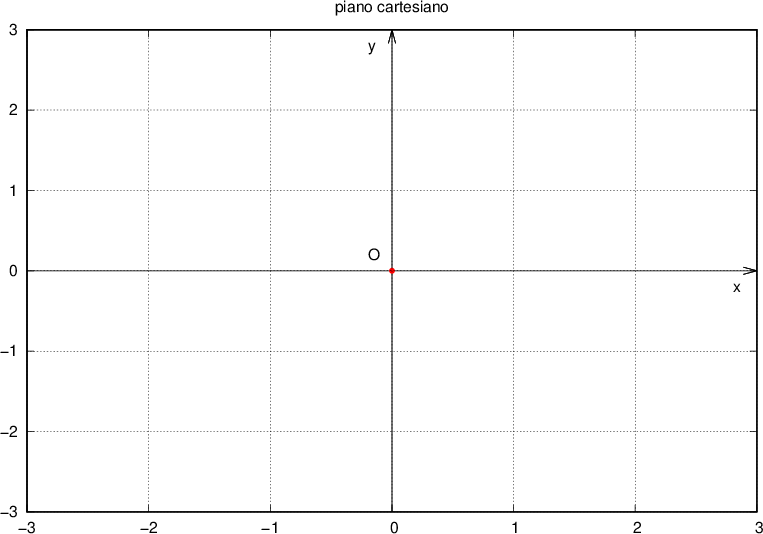
In questo modo otteniamo un piano cartesiano.
Nel seguente grafico rappresentiamo P il punto di coordinate (2; 1):
Per essere rigorosi: la griglia della battaglia navale ha un numero finito di possibili posizioni. Nel piano cartesiano le possibili posizioni invece sono infinite. Il ragionamento in linea di massima è lo stesso, sebbene in un sistema cartesiano abbiamo quasi sempre a che fare con quantità reali e non discrete e identifichiamo i punti di incrocio e non i quadrati delle caselle.
I quadranti
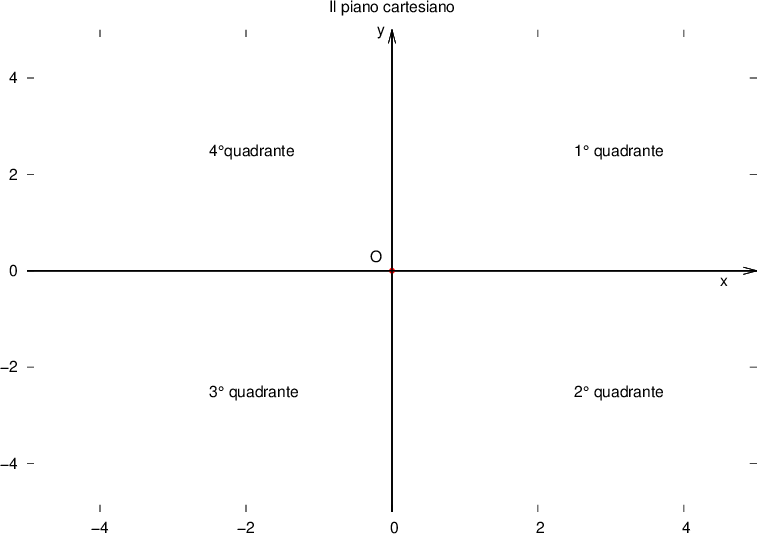
Il piano cartesiano è formato da due assi: uno orizzontale (asse delle ascisse) e uno verticale (asse delle ordinate). Entrambi gli assi sono rette orientate, ed essendo perpendicolari fra loro, le due rette si incontrano in un punto, detto origine O: convenzionalmente l'origine ha coordinate 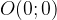 .
.
Un sistema siffatto è anche denominato xOy, indicando il nome dell'asse orizzontale, dell'origine e, infine, dell'asse verticale.
L'incrocio dei due assi divide il piano in quattro parti detti quadranti.
C'è una relazione diretta tra il quadrante in cui si trova un punto e il segno della sua ascissa e della sua ordinata, come rappresentato nella tabella:
Un punto sul piano cartesiano
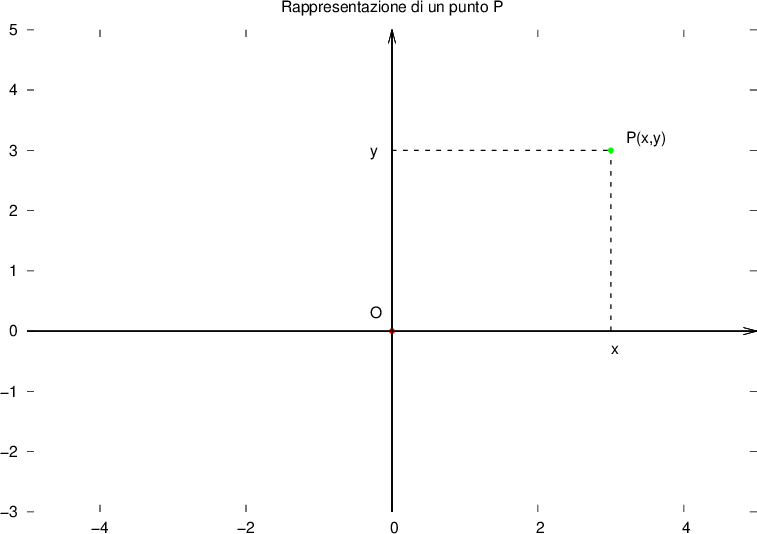
Un punto inserito in un piano cartesiano è determinato univocamente da due numeri reali, che si chiamano coordinate del punto P:
Questi due numeri ci dicono dove si trova il punto nel piano cartesiano. Il primo valore è l'ascissa e il secondo l'ordinata del punto.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Simmetrico di un punto
A partire dalle coordinate di un punto è possibile individuare il suo simmetrico sia rispetto all'asse x che rispetto all'asse y. Combinando le due simmetrie si ottiene la simmetria rispetto all'origine O del sistema di riferimento cartesiano.
Per fare il simmetrico di un punto rispetto all'asse delle x si mantiene la stessa ascissa e si inverte l'ordinata
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per fare il simmetrico di un punto rispetto all'asse delle y si mantiene la stessa ordinata e si inverte l'ascissa
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Per fare il simmetrico di un punto rispetto all'origine degli assi si invertono sia l'ascissa che l'ordinata
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Cambio di sistema di riferimento e traslazione
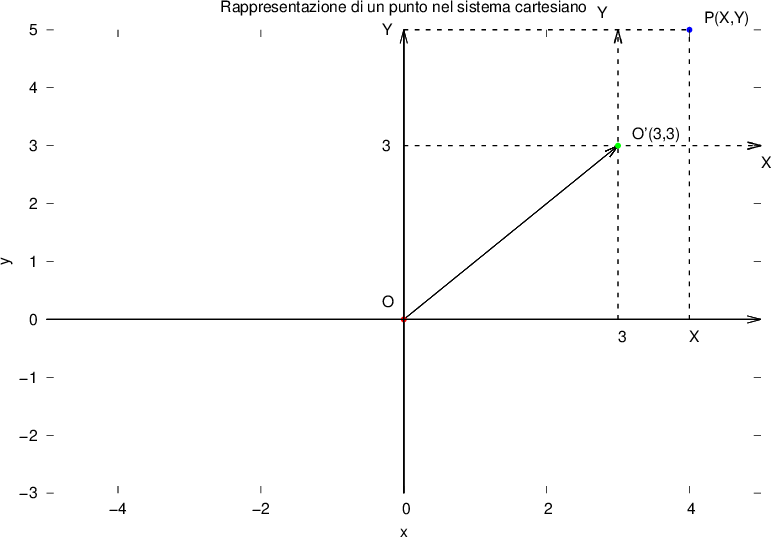
La scelta del'origine degli assi è del tutto arbitraria: a volte può essere comodo porre l'origine in punti opportuni, per rendere più agevoli calcoli o semplificare formule. Partendo dal nostro solito sistema di assi vediamo cosa succede se decidiamo di cambiare i nostri punti di riferimento: per esempio immaginiamo di porre, a partire dal grafico, l'origine nel punto O', di coordinate (3,3)
Le coordinate cartesiane rispetto a questo nuovo sistema di riferimento le indicheremo con lettere maiuscole, pertanto il sistema sarà del tipo XO'Y.
Per rendere chiaro lo svolgimento:
le variabili X e Y maiuscole si riferiscono al nuovo sistema di riferimento;
le variabili x e y minuscolo al solito sistema utilizzato finora.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Il vettore tra O e O' è il vettore di traslazione.
O', che nel vecchio sistema di riferimento aveva coordinate x = 3 e x = 3 ora diventa origine, pertanto avrà coordinate X = 0 e Y = 0.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Pertanto, indicando genericamente le coordinate del vettore di traslazione come 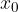 e
e 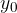 (nel caso in esempio entrambe uguali a 3) si hanno le seguenti relazioni:
(nel caso in esempio entrambe uguali a 3) si hanno le seguenti relazioni:
La nuova coordinata è uguale alla vecchia coordinata meno la posizione della nuova origine espressa nelle vecchie coordinate.
Vediamo ora se le relazioni ricavate in maniera molto semplice per quanto riguarda l'origine degli assi, sono valide per un generico punto P dello spazio.
E' semplice, partendo dal grafico, notare che le coordinate x e y del punto P nel vecchio sistema di assi cartesiani non sono altro che la somma delle x e y della nuova origine nel vecchio sistema e le coordinate del punto P nel nuovo sistema.
Valgono le seguenti relazioni:
Queste sono le relazioni per tornare alle coordinate nel vecchio sistema di assi cartesiani; per trovare invece la relazione che ci porta a trovare le nuove coordinate a partire dalle vecchie isoliamo la X e la Y al primo membro delle equazioni scritte sopra:
Luoghi di punti nel piano
Ora che sapete come disegnare un punto in un sistema di coordinate rettangolare, vedremo alcuni esempi di come disegnare luoghi di punti nel piano. Diamo un'occhiata ad alcuni esempi di base.
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »





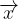 e
e 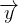 , di origine
, di origine 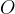 , si indica brevemente con
, si indica brevemente con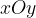
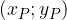 costituita dalle coordinate di P: la coordinata
costituita dalle coordinate di P: la coordinata 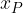 di un punto è la distanza del punto dall'asse y, e può avere segno positivo o negativo a seconda che P si trovi "a destra" o "a sinistra" dell'asse y; la coordinata
di un punto è la distanza del punto dall'asse y, e può avere segno positivo o negativo a seconda che P si trovi "a destra" o "a sinistra" dell'asse y; la coordinata 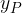 di un punto è la distanza del punto dall'asse x, e può avere segno positivo o negativo a seconda che P si trovi "sopra" o "sotto" l'asse y.
di un punto è la distanza del punto dall'asse x, e può avere segno positivo o negativo a seconda che P si trovi "sopra" o "sotto" l'asse y.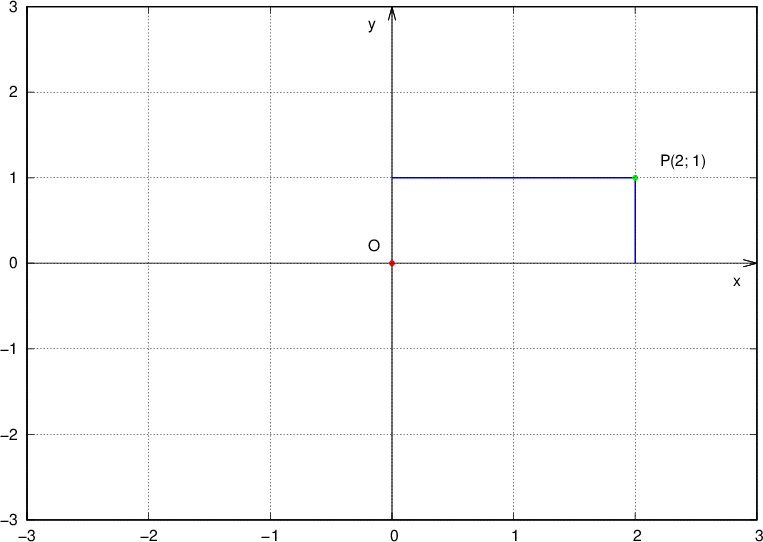
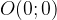 .
.
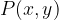
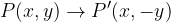
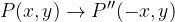
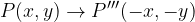
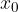 e
e 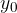 (nel caso in esempio entrambe uguali a 3) si hanno le seguenti relazioni:
(nel caso in esempio entrambe uguali a 3) si hanno le seguenti relazioni: