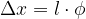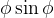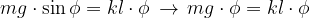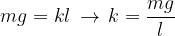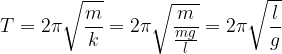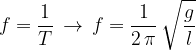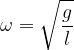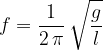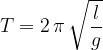Un pendolo è costituito da un filo alla cui estremità è attaccato un peso. Molti oggetti di uso comune possono essere visti come dei pendoli: da un semplice lampadario appeso al soffitto, alla pendola di un orologio a pendolo.
Una leggenda racconta che fu proprio grazie alle oscillazioni di un lume nel Duomo di Pisa che nel 1583 Galileo intuì le leggi che governano il moto di un pendolo.
Il pendolo semplice
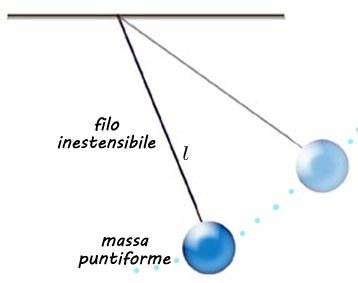
Per studiare le proprietà del pendolo introduciamo il pendolo semplice (o pendolo matematico). Il pendolo semplice è formato da:
un filo sottile e inestensibile di massa trascurabile
una massa puntiforme attaccata al filo
un supporto che sostiene il filo
Supponiamo che il baricentro del sistema coincida con il baricentro della massa puntiforme.
Immaginiamo di spostare la massa appesa al filo dalla posizione di equilibrio e di abbandonarlo. La massa (e quindi il baricentro del sistema) comincerà a oscillare lungo una traiettoria che disegna un arco di cerchio di raggio l.
Il raggio l è la lunghezza del pendolo.
Il periodo T del pendolo è l’intervallo di tempo impiegato a compiere un’oscillazione completa (avanti e indietro).
Se l’angolo descritto dal filo nello spostamento iniziale è molto piccolo (inferiore a circa 3°), le oscillazioni sono armoniche.
Descrizione matematica del pendolo
Se provassimo a misurare il periodo di oscillazione di un pendolo lungo l e di un pendolo più corto, si vedrebbe che la durata delle oscillazioni diminuisce. Possiamo pensare quindi che il periodo non dipenda dall'ampiezza dell'oscillazione ma dalla lunghezza del pendolo.
Cerchiamo che relazione lega il periodo di oscillazione T e la lunghezza l del filo.
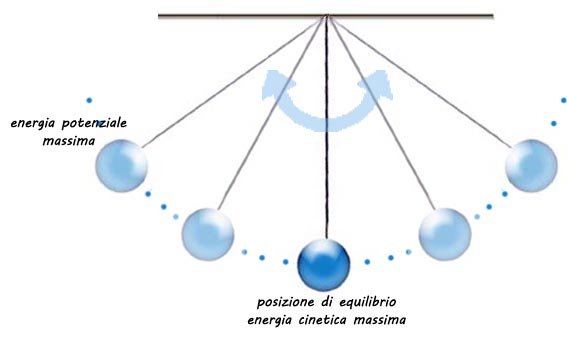
Osserviamo il fenomeno dal punto di vista energetico. Quando il pendolo si trova in alto ha la massima energia potenziale. Via Via che torna alla posizione di equilibrio (in basso), l'energia potenziale si trasforma in energia cinetica, e successivamente in energia potenziale mentre si allontana dalla posizione di equilibrio. Si ha quindi una trasformazione periodica di energia potenziale gravitazionale in energia cinetica, e viceversa.
Frequenza e periodo
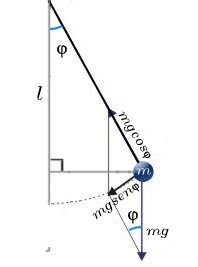
Osserviamo la figura, sappiamo che il pendolo ha una massa (considerata puntiforme) m perciò sul pendolo agirà una forza peso mg.
Scomponiamo la forza peso nelle due componenti:
Componente parallela al filo: 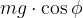
Componente perpendicolare al filo: 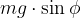
Vediamo che la componente perpendicolare al filo è rivolta verso il punto di equilibrio (sempre in ogni istante dell'oscillazione). Si tratta di una forza di richiamo analoga a quella delle molle per le quali vale 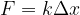
Poniamo quindi la componente pari alla forza di richiamo:
Osserviamo di nuovo l'immagine per ricavare lo spostamento 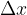 , che sarebbe lo spazio (l'arco di circonferenza) che il pendolo deve percorrere per tornare al punto di equilibrio:
, che sarebbe lo spazio (l'arco di circonferenza) che il pendolo deve percorrere per tornare al punto di equilibrio:
Dal momento che stiamo trattando angoli molto piccoli possiamo approssimare l'angolo col suo seno:
Sostituiamo nella precedente relazione:
Semplifichiamo e ricaviamo la costante k:
Sostituiamo la costante nell'espressione del periodo del moto armonico tipico della molla e ricaviamo il periodo del pendolo:
Possiamo notare, quindi, che il periodo d’oscillazione del pendolo non dipende né dalla sua massa, né dalla sua ampiezza, ma soltanto dalla sua lunghezza e dall'accelerazione di gravità.
La frequenza è il reciproco del periodo:
Relazione fra il periodo del pendolo e la lunghezza
Il periodo di oscillazione del pendolo non dipende dall'ampiezza di oscillazione ma dalla lunghezza del filo e dall'accelerazione di gravità. Accorciando il filo, la durata delle oscillazioni diminuisce.





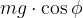
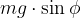
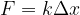
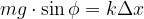
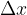 , che sarebbe lo spazio (l'arco di circonferenza) che il pendolo deve percorrere per tornare al punto di equilibrio:
, che sarebbe lo spazio (l'arco di circonferenza) che il pendolo deve percorrere per tornare al punto di equilibrio: