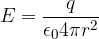Il campo elettrico
Per esplorare le proprietà del punto 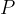 utilizziamo una carica di prova positiva
utilizziamo una carica di prova positiva 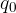 , cioè una carica positiva tanto piccola da non alterare in modo significativo le caratteristiche della distribuzione di cariche.
, cioè una carica positiva tanto piccola da non alterare in modo significativo le caratteristiche della distribuzione di cariche.
e si misura in Newton su Coulomb 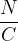
Rappresentazione del campo elettrico
Rappresentare graficamente il campo elettrico in un punto dello spazio è semplice: basta tracciare un vettore. Diversa è la situazione nel caso del campo elettrico in una regione estesa nella quale non è certo possibile tracciare un vettore per ogni punto.
In questi casi l’andamento del campo elettrico si visualizza mediante linee di forza, cioè curve che in un determinato punto 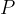 risultino tangenti al campo elettrico in quel punto medesimo.
risultino tangenti al campo elettrico in quel punto medesimo.
Esempi elementari
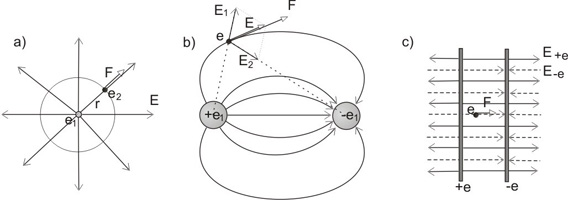
(fig. 2) Linee di forza di un campo elettrico radiale a), dipolo elettrico, b) piani paralleli di carica c)
Nella figura precedente sono evidenziate le linee di forza di alcuni campi elettrici elementari. In particolare:
campo elettrico radiale di una carica puntiforme: le linee di forza sono semirette con origine sulla carica (fig. a);
campo elettrico generato da due cariche puntiformi (dipolo elettrico) di segno opposto: le linee di forza del campo elettrico sono mostrate in figura b);
campo elettrico generato da due superfici piane parallele cariche ed opposte (condensatore piano): in questo caso si suppone che i piani di cariche siano infiniti (fig. c).
Tangenza e densità delle linee di forza
Le linee di forza escono sempre perpendicolarmente dal corpo carico positivamente e terminano perpendicolarmente nel corpo carico negativamente. L'unica condizione è che la carica sul corpo sia statica.
Dove l'intensità del campo elettrico è più forte la densità delle linee di forza sarà maggiore e viceversa, come illustrato in figura 3.
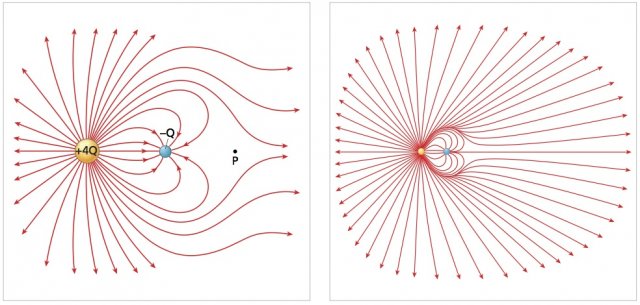
(fig. 3) Linee di forza del campo elettrico
Flusso del campo elettrico
Consideriamo una superficie piana S. Il vettore area 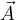 di una superficie piana S è un vettore che ha
di una superficie piana S è un vettore che ha
modulo uguale all’area A della superficie;
direzione perpendicolare alla superficie.
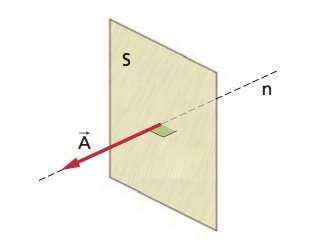
Vettore area di una superficie piana
Consideriamo una superficie piana S immersa in un campo elettrico uniforme 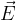 : in ciascun punto di S è definito un vettore
: in ciascun punto di S è definito un vettore 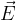 .
.
Il flusso del campo elettrico uniforme 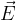 , attraverso la superficie piana S, di vettore area
, attraverso la superficie piana S, di vettore area 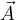 è
è
dove 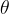 è l’angolo fra il campo e la normale alla superficie (vedi figura).
è l’angolo fra il campo e la normale alla superficie (vedi figura).
L'unità di misura del flusso risulta 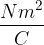
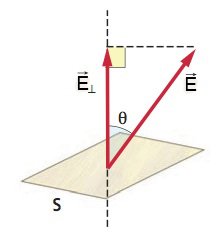
Flusso del campo elettrico
A questo punto vanno fatte alcune precisazioni:
il flusso del campo elettrico è uno scalare nonostante derivi dal prodotto di due vettori (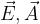 );
);
nella (1) il termine 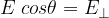 rappresenta il modulo della componente del campo E perpendicolare alla superficie;
rappresenta il modulo della componente del campo E perpendicolare alla superficie;
il segno del flusso dipende dall'angolo 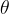 (vedi esempio sottostante).
(vedi esempio sottostante).
Teorema di Gauss
Carl Friedrich Gauss dimostrò che il flusso del campo elettrico gode di una importante proprietà, nota come teorema del flusso:
il flusso 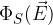 del campo elettrico attraverso una superficie chiusa S è
del campo elettrico attraverso una superficie chiusa S è
dove 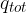 è la carica totale racchiusa dalla superficie S ed
è la carica totale racchiusa dalla superficie S ed  è la costante dielettrica del mezzo (*).
è la costante dielettrica del mezzo (*).
(*) La costante dielettrica assoluta e relativa di un mezzo è stata trattata nel capitolo Forza di Coulomb.
Applicazione a corpi carichi
Sfruttiamo il teorema di Gauss per il calcolo dell'intensità del campo elettrico in quattro casi particolari di corpi carichi elettricamente immersi nel vuoto.
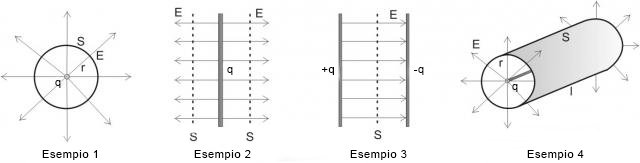
Intensità del campo elettrico generato da una carica puntiforme, da un piano di carica, da due piastre cariche parallele fra loro e da un filo rettilineo elettricamente carico
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Esempio
Gli esempi sono visibili solo per gli utenti registrati
Registrati per vedere gli esempi »
Per l'accesso gratuito agli esercizi è necessario compilare il tuo profilo.
Completa il tuo profilo »
Sfera cava elettricamente carica
Consideriamo una sfera metallica cava di raggio R di carica q. La densità di carica sulla superficie della sfera è 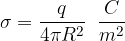 .
.
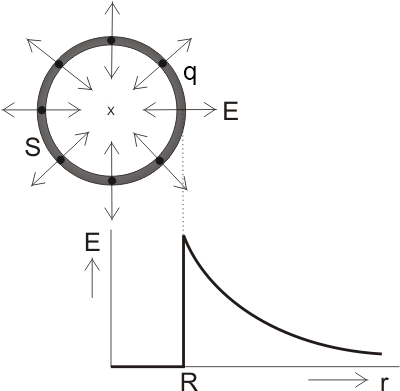
Andamento di E in una sfera cava elettricamente carica
All'interno della sfera (r < R) l'intensità del campo elettrico è nulla poiché non vi sono cariche (basta applicare il teorema di Gauss come nell'esempio 1 della sezione precedente). Per r > R, invece, si ritrova l'espressione del campo elettrico di una carica puntiforme




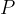 la proprietà di esercitare una forza
la proprietà di esercitare una forza 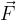 su una carica
su una carica 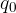 collocata in esso.
collocata in esso.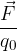 è indipendente da
è indipendente da 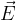 , generato da una distribuzione di cariche nel punto
, generato da una distribuzione di cariche nel punto 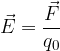
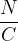
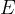 è quella di una forza per unità di carica (newton su coulomb,
è quella di una forza per unità di carica (newton su coulomb, 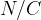 ); vedremo più avanti nella sezione dedicata al potenziale elettrico che
); vedremo più avanti nella sezione dedicata al potenziale elettrico che 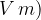 .
.

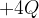 , dove le linee sono molto dense, mentre è praticamente nullo attorno al punto
, dove le linee sono molto dense, mentre è praticamente nullo attorno al punto 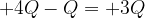 .
.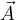 di una superficie piana S è un vettore che ha
di una superficie piana S è un vettore che ha
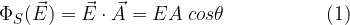
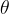 è l’angolo fra il campo e la normale alla superficie (vedi figura).
è l’angolo fra il campo e la normale alla superficie (vedi figura).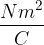

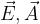 );
);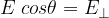 rappresenta il modulo della componente del campo E perpendicolare alla superficie;
rappresenta il modulo della componente del campo E perpendicolare alla superficie;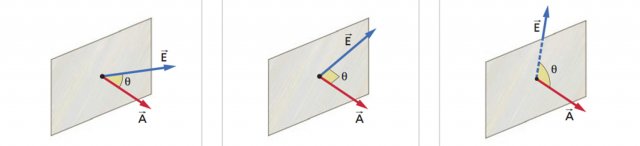
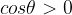 cioè se
cioè se 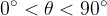 ; esso è nullo per
; esso è nullo per 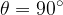 ed è negativo se
ed è negativo se 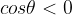 ossia se
ossia se 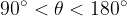
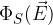 del campo elettrico attraverso una superficie chiusa S è
del campo elettrico attraverso una superficie chiusa S è
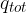 è la carica totale racchiusa dalla superficie S ed
è la carica totale racchiusa dalla superficie S ed  è la costante dielettrica del mezzo (*).
è la costante dielettrica del mezzo (*).
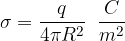 .
.